Number : Real Numbers

Instructional Tools & Strategies

The selection of instructional tools and strategies by teachers must be thoughtful and purposeful, based on the context, intention, and learning goals. In doing so, teachers model and positively influence students’ ability to choose tools, technology, and strategies when they perform, illustrate, and explain mathematical ideas and their mathematical thinking.

All students should be encouraged to select and use tools to illustrate mathematical ideas. Students come to understand that making their own representations is a powerful means of building understanding and of explaining their thinking to others.

When representing numbers and their operations, various tools can be used depending on the type of model.

Type of Model	Tools	Examples
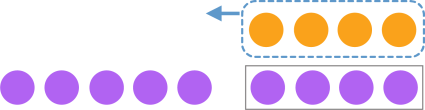
Set	Base ten blocks Colour tiles Integer tiles Two-colour counters Linking cubes Pattern blocks	$(+5) – (–4) = (+9)$ Start with +5. Then, so that $(–4)$ can be removed, use the zero principle to add 4 zero pairs, resulting in an additional $+4$ and therefore $+9$ in all.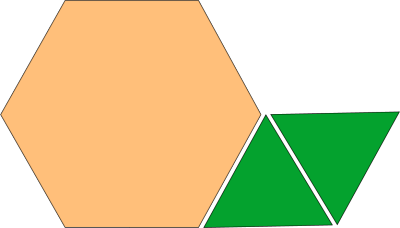 $\frac{2}{3}$ of the set of blocks are green.
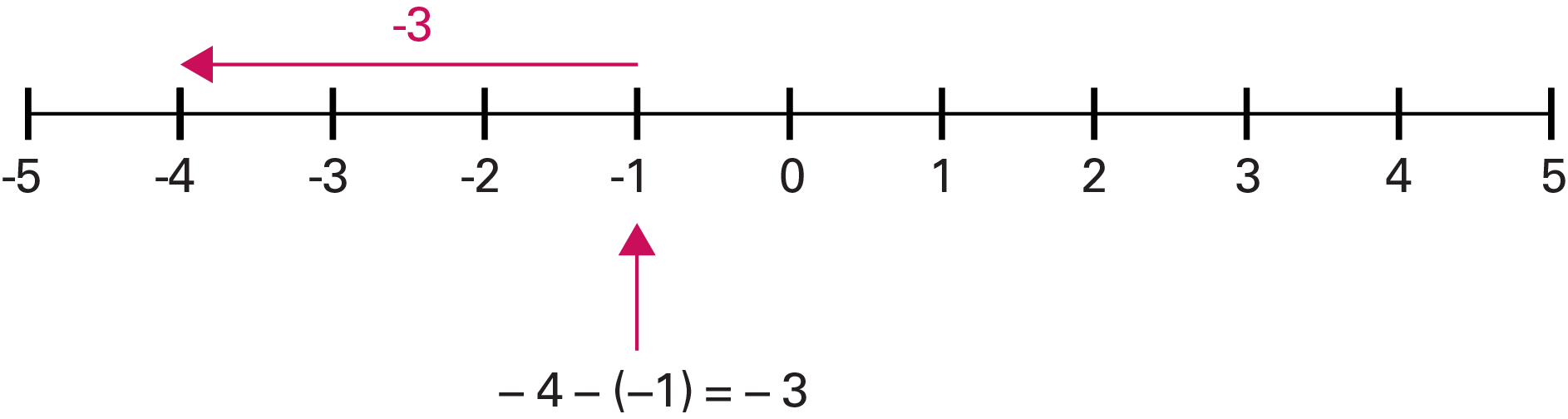
Linear	Number line Double number line Measuring tape Linear strips (for example, fraction strips) or rods (relational rods) Geoboards	Above, a red arrow points from minus 1 to minus 4. It says: minus 3. Under, a red arrow points to minus 1. It says: minus 4 minus opening parenthesis minus 1 closing parenthesis equals minus 3. What is the distance between $(-1)$ and $(-4)$ if I start from $(-1)$ and end up at $(-4)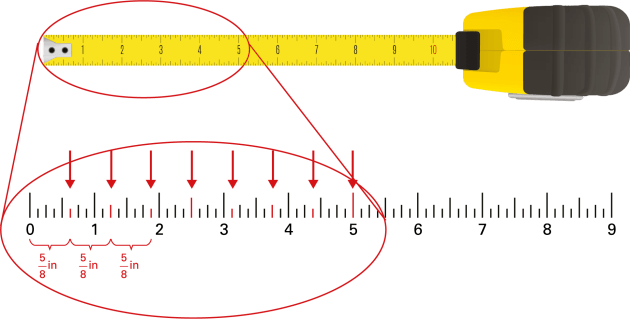$? The first 5 inches are circled in red. Below is a zoomed-in representation of the first 5 inches. The inches are divided into 8 hash marks. A red arrow appears over each fifth hash mark, and those hash marks are also in red. Below, the fraction five eighths appears three times to indicate the first three red marks. How many $\frac{5}{8}$ inch in 3 feet?
Area	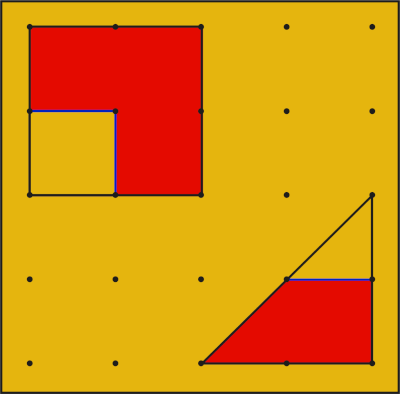Geoboards Grids Square tiles, colour tiles Pattern blocks Rods (relational rods)	$\frac{3}{4}$ of each shape is red. - One exponent 2: One stick with a length equivalent to 1 cube. - 2 exponent 2: 2 sticks, each with a length of 2 cubes. - 3 exponent 2: 3 sticks, each with a length of 3 cubes. - 4 exponent 2: 4 sticks, each with a length of 4 cubes. - 5 exponent 2: 5 sticks, each with a length of 5 cubes. - 6 exponent 2: 6 sticks, each with a length of 6 cubes. - 7 exponent 2: 7 sticks, each with a length of 7 cubes. - 8 exponent 2: 8 sticks, each with a length of 8 cubes. - 9 exponent 2: 9 sticks, each with a length of 9 cubes. - Ten exponent 2: ten sticks, each with a length of 10 cubes. Pattern to explore a conceptual understanding of the power rules.
Volume	Linking cubes Measuring cup	Compare volumes when one of the dimensions changes.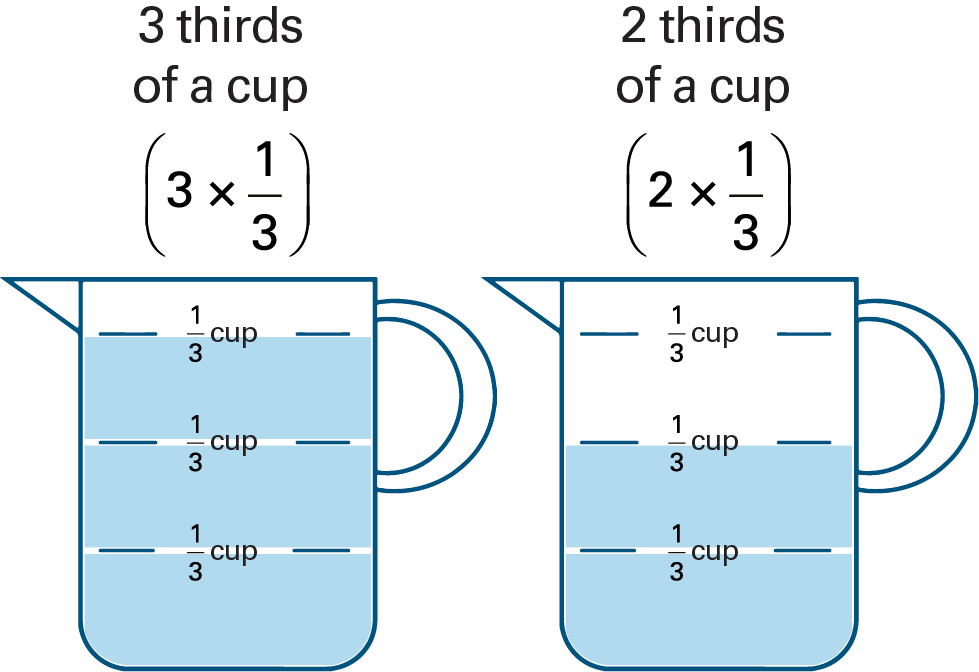 The first cup is three-thirds full. Above, it says: “3 thirds of a cup. Opening parenthesis, 3 times one third, closing parenthesis”. The second cup is two-thirds full. Above, it says: “2 thirds of a cup. Opening parenthesis, 2 times one third, closing parenthesis”. $1\frac{2}{3}$ represented with unit fractions using capacity.

Example using fraction strips:

A baker sells $\frac{3}{8}$ of her loaves of bread in the morning and $\frac{1}{2}$ of her loaves of bread during the rest of the day. At closing time, she has 11 loaves of bread left. How many loaves of bread did she have when the store opened?

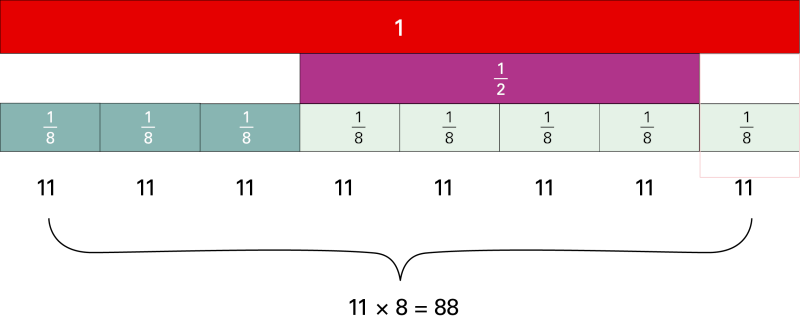
$A strip of fractions represents the equation eleven multiplied by 8 equals 88.$

Therefore, we can see from the representation that the baker has $\frac{1}{8}$ of her loaves of bread left, which we know is 11 loaves. Since $\frac{1}{8}$ is equivalent to 11 loaves of bread, she must have had $11 \ × 8 \ = 88$ loaves of bread when the store opened.

Reflection

How can technology help students create accurate models and draw relevant conclusions?
How can the use of technology stimulate the development of students’ critical and creative thinking in relation to the numerous data they encounter in their daily lives?

Type of Model	Tools	Examples
Set	Base ten blocks Colour tiles Integer tiles Two-colour counters Linking cubes Pattern blocks	\((+5) – (–4) = (+9)\) Start with +5. Then, so that \((–4)\) can be removed, use the zero principle to add 4 zero pairs, resulting in an additional \(+4\) and therefore \(+9\) in all. \(\frac{2}{3}\) of the set of blocks are green.
Linear	Number line Double number line Measuring tape Linear strips (for example, fraction strips) or rods (relational rods) Geoboards	Above, a red arrow points from minus 1 to minus 4. It says: minus 3. Under, a red arrow points to minus 1. It says: minus 4 minus opening parenthesis minus 1 closing parenthesis equals minus 3. What is the distance between \((-1)\) and \((-4)\) if I start from \((-1)\) and end up at \((-4)\)? The first 5 inches are circled in red. Below is a zoomed-in representation of the first 5 inches. The inches are divided into 8 hash marks. A red arrow appears over each fifth hash mark, and those hash marks are also in red. Below, the fraction five eighths appears three times to indicate the first three red marks. How many \(\frac{5}{8}\) inch in 3 feet?
Area	Geoboards Grids Square tiles, colour tiles Pattern blocks Rods (relational rods)	\(\frac{3}{4}\) of each shape is red. - One exponent 2: One stick with a length equivalent to 1 cube. - 2 exponent 2: 2 sticks, each with a length of 2 cubes. - 3 exponent 2: 3 sticks, each with a length of 3 cubes. - 4 exponent 2: 4 sticks, each with a length of 4 cubes. - 5 exponent 2: 5 sticks, each with a length of 5 cubes. - 6 exponent 2: 6 sticks, each with a length of 6 cubes. - 7 exponent 2: 7 sticks, each with a length of 7 cubes. - 8 exponent 2: 8 sticks, each with a length of 8 cubes. - 9 exponent 2: 9 sticks, each with a length of 9 cubes. - Ten exponent 2: ten sticks, each with a length of 10 cubes. Pattern to explore a conceptual understanding of the power rules.
Volume	Linking cubes Measuring cup	Compare volumes when one of the dimensions changes. The first cup is three-thirds full. Above, it says: “3 thirds of a cup. Opening parenthesis, 3 times one third, closing parenthesis”. The second cup is two-thirds full. Above, it says: “2 thirds of a cup. Opening parenthesis, 2 times one third, closing parenthesis”. \(1\frac{2}{3}\) represented with unit fractions using capacity.