Algebra : Expressions, Equations, and Inequalities
Connections Across Grades
The progression of algebra learning expectations from one grade level to the next allows students to develop their algebraic reasoning and a conceptual understanding of variables, algebraic expressions, equations, and inequalities.
Some notable differences lie in the types of numbers and the complexity of expressions that students must manipulate. The examples in the following tables reflect this progression.
Algebraic expressions
Specific Expectation: C2.1
Mathematical Processes: Selecting Tools and Strategies; Representing
Represent the addition of these monomials using at least one concrete and one pictorial representation.
\(3m + 2n + 4n + 5m\)
Specific Expectation: C2.1
Mathematical Processes: Selecting Tools and Strategies; Representing
Represent the operations of these monomials using at least one concrete and one pictorial representation.
\(3m – 2n + 4n – 5m\)
Specific Expectation: C2.1
Mathematical Processes: Selecting Tools and Strategies; Representing
Represent these operations using at least one concrete and one pictorial representation.
- \(-3m+ -2n+4n – 5m \)
- \((-3a + 2b) + (4a + -3b)\)
Specific Expectations: C1.2, 1.3, 1.4
Mathematical Process: Selecting Tools and Strategies
Simplify this algebraic expression using at least 2 strategies.
\(-3x\,(4x – 3) – 5\,(4x^2 – 6x + 7)\)
Evaluating Algebraic Expressions
Specific Expectation: C2.2
Mathematical Process: Selecting Tools and Strategies
Given that the perimeter of a rectangle can be determined using the formula \(P=2b+2h\), determine the perimeter of a rectangle with a base of 12.5 cm and a height of 45.2 cm.
Specific Expectation: C2.2
Mathematical Process: Selecting Tools and Strategies
The rental cost of various skateboards at the store Riding Together can be calculated using the following formula: \(C=50+ph\), where \(p\) represents the cost per hour for the type of skateboard rented, and \(h\) is the rental duration in hours.
What will be the total cost to rent a skateboard that costs $4.25 per hour for 5 hours?
Specific Expectation: C2.2
Mathematical Process: Selecting Tools and Strategies
Evaluate the expression \(3\left(\frac{1}{3}a+b\right)\) if \(a=\frac{3}{4}\) and \(b=\frac{5}{3}\).
Specific Expectation: C1.5
Mathematical Process: Selecting Tools and Strategies
Determine if the point \(\left(\frac{7}{5},\frac{6}{5}\right)\) is on the line defined by the equation \(y=-\frac{3}{5}x+2\).
Algebraic Equations
Specific Expectation: C2.3
Mathematical Process: Reasoning and Proving
Amid got 9 as the solution to this equation, while Marcie got 3. Who’s correct and how do you know? \(4a-12=15+9\)
Specific Expectation: C2.3
Mathematical Process: Reasoning and Proving
Without solving the equation, how can you know that the solution must be a negative value?
\(5x+12=3x+4\)
Specific Expectation: C2.3
Mathematical Process: Reasoning and Proving
What would be a good estimate of the value of \(x\) for the equation \(29x−59=61x+28\) to be true? Explain your reasoning.
Specific Expectation: C4.2
Mathematical Process: Representing
Represent all combinations of 2 numbers, \(x\) and \(y\), for which \(2x+y=24\).
Algebraic Inequalities
Specific Expectation: C2.4
Mathematical Process: Communication
Write a scenario that could be represented by this inequality.
\(2m+3 ≥ 15\)
Specific Expectation: C2.4
Mathematical Process: Reflecting
Write an inequality with at least 4 terms whose solution can be represented by this orange ray.

Specific Expectation: C2.4
Mathematical Process: Reflecting
Which of these rays represents the solution to the inequality \(3x-5<2x-3\)? How do you know?
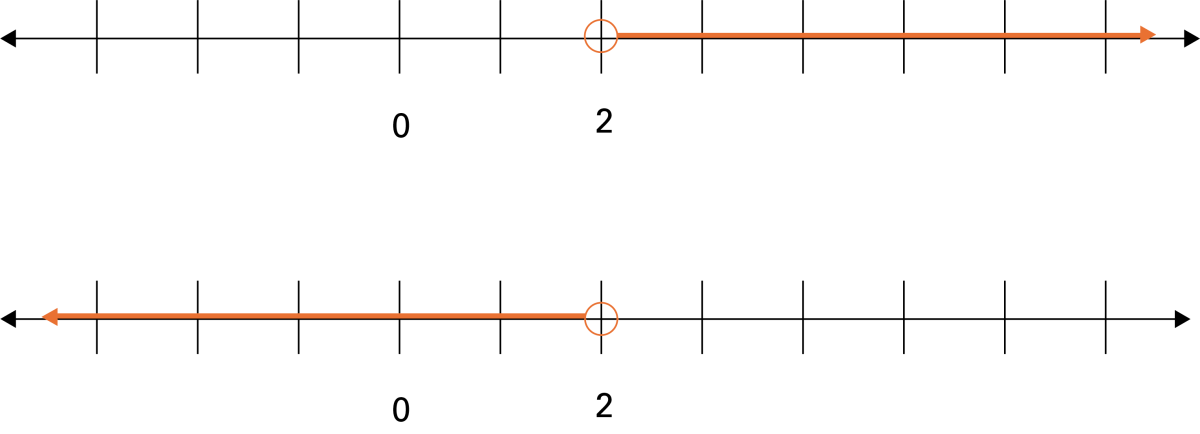
The points zero and two are identified. The point two is circled, and an orange arrow starts from this point and extends to the right. A second number line is marked. The points zero and two are identified. The point two is circled, and an orange arrow starts from this point and extends to the left.
Specific Expectation: C4.2
Mathematical Process: Reflecting
Which of these two inequalities will have the most solutions? How do you know?
\(2x>36\) or \(2x\ge 36\)
Reflection
- How does students’ prior knowledge influence their understanding of Grade 9 algebraic concepts, and how can this knowledge be used to promote deeper learning of algebraic concepts?
- How do different pedagogical practices influence the development of algebraic reasoning, and what specific strategies can maximize long-term impact that meets individual student needs?
