Algebra : Expressions, Equations, and Inequalities
Key Concepts
Algebraic Expressions
- Algebraic expressions are useful for generalizing various situations such as numerical patterns and growing patterns.
- There are an infinite number of equivalent algebraic expressions.
- The same situation can be represented by several equivalent algebraic expressions, but each often tells a different story.
- An algebraic expression consists of constants and variables connected by mathematical operation symbols. It does not include equality or inequality signs (for example, \(n\left(n-1\right)+4\), \(\frac{-7}{x}+1{.}5\)). Each element separated by an addition or subtraction is a term.
- A coefficient is a multiplier placed in front of the variable(s) of a term.
- Similar terms differ only by their coefficient (for example, \(3ab^2\) and \(-ab^2\), \(-\frac{3}{4}x\) and \(x\)). They can be added or subtracted.
- A monomial consists of a single term, which can be a number (constant) or the product of a coefficient and variables whose exponents are natural numbers (for example, \(4,\ 3x,\ \frac{3b}{4},\ 4p^3rt^2\)).
- Polynomials are a particular type of algebraic expression consisted of a sum of several terms, which are exclusively monomials. A binomial is the sum of two monomials (for example, \(3{.}5x-5{.}2\)) and a trinomial is the sum of three monomials (for example, \(4x^2+12x-5\)).
The following table summarizes how an understanding of algebraic expressions is developed within each grade.
| Grade Level | Knowledge and Skills | Types of Numbers |
|---|---|---|
| 4 | Use of symbols (icons and letters) as variables in algebraic expressions | |
| 5 | Describe equivalent relationships | |
| Evaluate algebraic expressions | Whole numbers | |
| 6 | Add monomials with a degree of 1 | Whole numbers |
| Evaluate algebraic expressions | Whole numbers and decimal tenths | |
| 7 | Add and subtract monomials with a degree of 1 | Whole numbers |
| Evaluate algebraic expressions | Whole numbers and decimal numbers | |
| 8 |
Add and subtract monomials with a degree of 1
Add binomials with a degree of 1 |
Integers |
| Evaluate algebraic expressions | Rational numbers | |
| 9 | Create, compare and simplify algebraic expressions | Real numbers |
Equations
- An equation is a mathematical statement consisting of one or more variables and the equality symbol. It expresses an equality between two algebraic expressions.
- Some equations have a finite number of solutions, while others have an infinite number of solutions or no solution.
- A single-variable equation has one variable, called the unknown, and the solution is the value or values of the unknown that make the equality true. It can have:
- A finite number of solutions (for example, \(3\left(4x-5\right)=8x+11\), \(\frac{2}{3}x+\frac{3}{5}=\frac{5}{6}x-\frac{4}{5}\)).
- An infinite number of solutions (for example, \(2x+4=2\left(x+2\right)\)).
- No solution (for example, \(2x+4=2x+5\)).
- A two-variable equation expresses the relationship between the two variables. There can be an infinite number of values for the variables as long as the relationship is maintained (for example, \(C=12h+35\), \(y=-3x+12\), \(x+y=24\)).
- A formula is a general expression that contains several variables describing a relationship that is always true (for example, \(V=\frac{1}{3}\pi r^2h\), \(F=\frac{9}{5}C+32\)).
- An identity is an equation that expresses the equality between two equivalent algebraic expressions. This equality is always true, regardless of the value of the variable (for example, \(3x+5x=8x\), \(2x\left(3x-5\right)=6x^2-10x\)).
- A single-variable equation has one variable, called the unknown, and the solution is the value or values of the unknown that make the equality true. It can have:
- A variety of tools, representations or strategies can be used to solve an equation. Some are more appropriate depending on the context or type of equation.
The following table summarizes the types of numbers used as well as the complexity level of the equations to be solved for each grade level.
| Grade Level | Types of Equations | Types of Numbers |
|---|---|---|
| 4 | \begin{align}12 + a + 7 &= 32 + 17 \\ 40 − 15 &= 2 \times n − 5\end{align} | Whole numbers up to 50 |
| 5 | \begin{align}52 + a + 27 &= 72 + 17 \\ 80 − 24 &= 2n − 48\end{align} | Whole numbers up to 100 |
| 6 | \begin{align}80 − 24 &= 2n + 4n \\ 5a + 2a &= 109 − 25\end{align} | Whole numbers |
| 7 | \begin{align}3m + 5m &= 98 + 62 \\ 4.5p + 2.3p &= 14.7 + 12.5\end{align} | Whole numbers and decimal numbers |
| 8 | \begin{align}−5x − 7x &= −40 − (−4) \\ 4.5p − 12.7 &= 2.3p + 4.9 \\ 132 &= x^2 + 122\end{align} | Integers and decimal numbers |
| 9 | \begin{align}3n + 42 &= −15 \\ −3(3x + 4) &= 7(−x − 5) \\ 23r − 4 &= 5r + 35\end{align} | Rational numbers |
Inequalities
- Inequalities are mathematical statements that include one of the inequality symbols:
- < is less than
- > is greater than
- ≤ is less than or equal to
- ≥ is greater than or equal to
- The solution to an inequality of the form a\(x\) + b\(y\) > k can be represented by a shaded region on a Cartesian plane, where the corresponding equation a\(x\) + b\(y\) = k forms its boundary. If the boundary line is part of the solution set, it will be solid; if it is not part of the solution, it will be dashed.
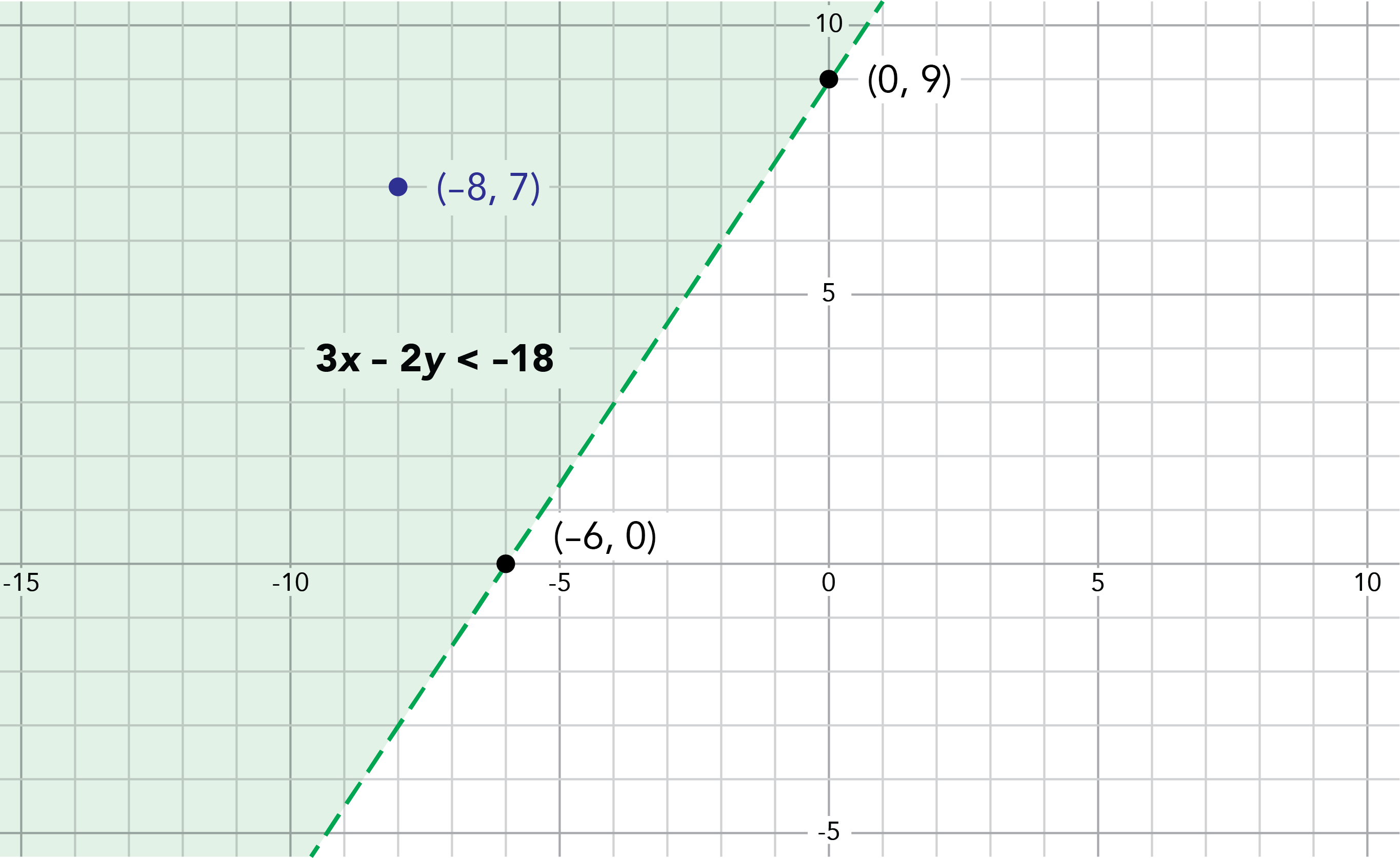
On the Cartesian plane numbered in increments of 5, the dotted line passes through the coordinates minus 6, 0 and 0, 9. In the shaded area, it says “3x minus 2y is smaller than minus 18”. A dot indicates the minus 8, 7 coordinate.
- The solution set of an inequality can be determined by substituting the coordinates of a point (for example, the point (-8, 7)) into the inequality. If the coordinates of the point satisfy the inequality, the point is part of the solution set and will be included in the shaded region on the graph.
- Solving inequalities allows us to model and solve real-world problems where values can vary within a certain range or must meet specific limits.
The following table summarizes the types of numbers used as well as the complexity level of the inequalities to be solved for each grade level starting from Grade 4, where inequalities are introduced.
| Grade Level | Types of Inequalities | Types of Numbers |
|---|---|---|
| 4 | \begin{align}a + 12 &≤ 20 \\ 18 − b &> 7\end{align} | Whole numbers up to 20 |
| 5 | \begin{align}n + 3 &< 9 \\ 3m &≥ 18\end{align} | Whole numbers up to 50 |
| 6 | \begin{align}3m − 8 &≥ 19 \\ 20 &< \frac{a}{3} + 7\end{align} | Whole numbers up to 100 |
| 7 | \begin{align}12c − 7c &≤ 13 + 27 \\ 35 + 29 &> 5x + 11x\end{align} | Whole numbers |
| 8 | \begin{align}−2p − 6p &< 17 + 15 \\ 5x − 12 &≥ 3x + 8\end{align} | Integers |
| 9 | \begin{align}−3y &< 27 \\ 2x + 3y &≥ 48\end{align} | Rational numbers |
Reflection
- How does a deep understanding of operations with numbers influence the ability to manipulate algebraic expressions and solve equations?
- What role does the development of algebraic reasoning play in understanding operations with algebraic expressions and equations?
- How does a deep understanding of equations enrich student approaches and effectiveness in solving inequalities?
- How do inequalities model real-world situations differently from equations, and what impact does this have on decision-making and problem-solving?
