Données : Ensemble de données à une et à deux variables
Outils et stratégies pédagogiques
Toutes et tous les élèves peuvent développer la capacité de sélectionner et d’utiliser les technologies et les stratégies appropriées pour représenter un ensemble de données. Le choix du bon type de diagramme pour représenter les données permet d’informer efficacement le public visé. Ainsi, la technologie aide à créer, à comparer et à modifier une variété de diagrammes en peu de temps et favorise une réflexion plus approfondie sur la pertinence, l’interprétation et les conclusions qui peuvent être tirées de l’ensemble des données. Ces quelques exemples représentent diverses situations.
| Contexte | Outils technologiques | Stratégies |
|---|---|---|
| Analyse d’un ensemble de données à une variable (par exemple, quantité de sucre contenu dans diverses boissons). |
|
|
| Analyse d’un ensemble de données à deux variables (par exemple, la relation entre la consommation d’essence d’une voiture et sa vitesse). |
|
|
| Analyse de plusieurs variables deux par deux (par exemple, la relation entre la longueur de différentes parties du corps). |
|
|
Le contexte et le type de données analysées vont déterminer les types de diagramme et de mesures de tendance centrale et de dispersion qui seront les plus appropriés. Ceux-ci influenceront les conclusions qui en seront tirées.
Exemple d’analyse d’un ensemble de données
Voici le nombre de points qui ont été marqués lors des 30 derniers matchs par deux joueurs de basketball d’une même équipe. L’entraîneur doit conserver seulement l’un des deux joueurs pour l’année prochaine. Lequel devrait-il garder et pourquoi?
Joueur A : 26, 32, 47, 15, 29, 18, 33, 32, 40, 21, 34, 45, 19, 36, 28, 34, 22, 43, 36, 26, 33, 18, 28, 32, 44, 35, 28, 22, 36, 40
Joueur B : 26, 28, 36, 34, 33, 28, 22, 25, 31, 34, 28, 27, 31, 25, 26, 32, 32, 29, 30, 26, 32, 34, 25, 24, 28, 25, 31, 29, 30, 27
| Moyenne | Médiane | Mode | |
|---|---|---|---|
| Joueur A | 31,07 | 32 | 32 |
| Joueur B | 28,93 | 28,5 | 28 |
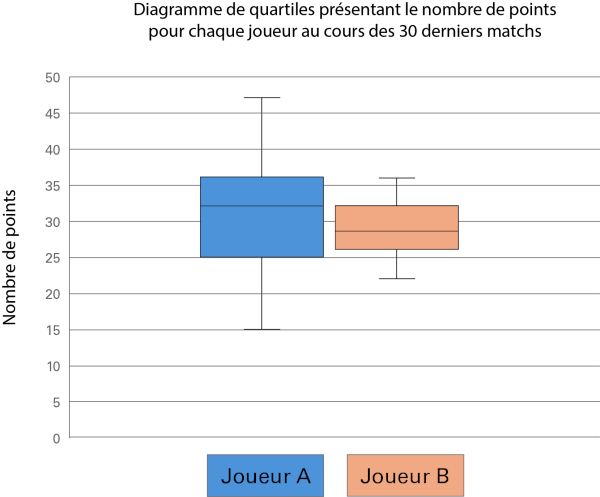
L’axe vertical représente le nombre de points de zéro à 50. Sur l’axe horizontal est représenté le joueur « A » et le joueur « B ». Les données du joueur « A » sont en bleues. Sa valeur minimale est 15, son premier quartile est à 25, la médiane à 32 et le troisième quartile à 36. Sa valeur maximale est 47. Les données du joueur « B » sont en orange. Sa valeur minimale est 23. Son premier quartile est 26. Sa médiane entre 28 et 29, et le troisième quartile à environ 32. Sa valeur maximale est 36.
Les mesures de tendance centrale montrent que Joueur A a obtenu généralement plus de points que Joueur B, alors que les diagrammes de quartiles montrent que Joueur B est plus constant que Joueur A au niveau des points marqués.
Réflexion
- Comment les outils technologiques peuvent-ils aider les élèves à créer des modèles précis et ainsi leur permettre de tirer des conclusions pertinentes?
- En quoi l’utilisation des outils technologiques peut-elle stimuler le développement de la pensée critique et créative des élèves face aux nombreuses données qu’elles et ils rencontrent dans leur vie quotidienne?
