Littératie financière : Appréciation et dépréciation
Liens avec les autres domaines
En offrant des contextes de littératie financière pour mettre en application les concepts appris dans les autres domaines, les élèves peuvent mieux comprendre la façon dont ces concepts sont interreliés. Les élèves développent alors une vision plus globale des mathématiques, font des liens pertinents avec la vie quotidienne et leur réalité et deviennent des mathématiciennes confiantes et des mathématiciens confiants.
Les exemples ci-dessous illustrent la manière dont la compréhension et l’application de la littératie financière peuvent être démontrés dans des contextes provenant des autres domaines.
En examinant chaque question, réfléchissez aux attentes et aux contenus d’apprentissages du domaine de Littératie financière dont les élèves ont besoin pour y répondre ainsi qu’aux liens avec les concepts clés.
Nombres : Pourcentage
Contenus d’apprentissage : B3.5, F1.4
Processus mathématiques : Résolution de problèmes
Il est recommandé de prévoir 32 % de son salaire annuel pour le logement. Une personne aux études ayant un salaire annuel de 12 400 $ peut se permettre de consacrer combien d’argent par mois pour louer un appartement?
Algèbre : Relations linéaires
Contenus d’apprentissage : C3.3, F1.4
Processus mathématiques : Réflexion, Représentations
Marie compare deux offres d’emploi. Le premier emploi offre un salaire de 14 $ de l’heure, avec une augmentation annuelle de 0,50 $ de l’heure. Le deuxième emploi offre un salaire de 13 $ de l’heure, avec une augmentation annuelle de 0,75 $ de l’heure.
- Si Marie prévoit conserver cet emploi pendant trois ans, quel emploi lui recommanderais-tu de choisir? Justifie ton choix.
- Marie travaille en moyenne 15 heures par semaine. Son salaire net est environ 85 % de son salaire brut. Elle désire économiser entre 12 000 et 15 000 $ pendant ses 3 années de travail. Elle doit aussi payer 65 $ par mois pour son téléphone cellulaire en plus de ses dépenses, comme l’achat de vêtements et les sorties avec ses amies et amis. Crée un budget possible pour Marie.
Données : Analyse de données
Contenus d’apprentissage : D1.2, F1.2
Processus mathématiques : Raisonnement et justification, Réflexion
La valeur d’une bande dessinée de collection basée sur son âge est représentée par ce nuage de points ainsi qu’un modèle de régression approprié aux données recueillies.
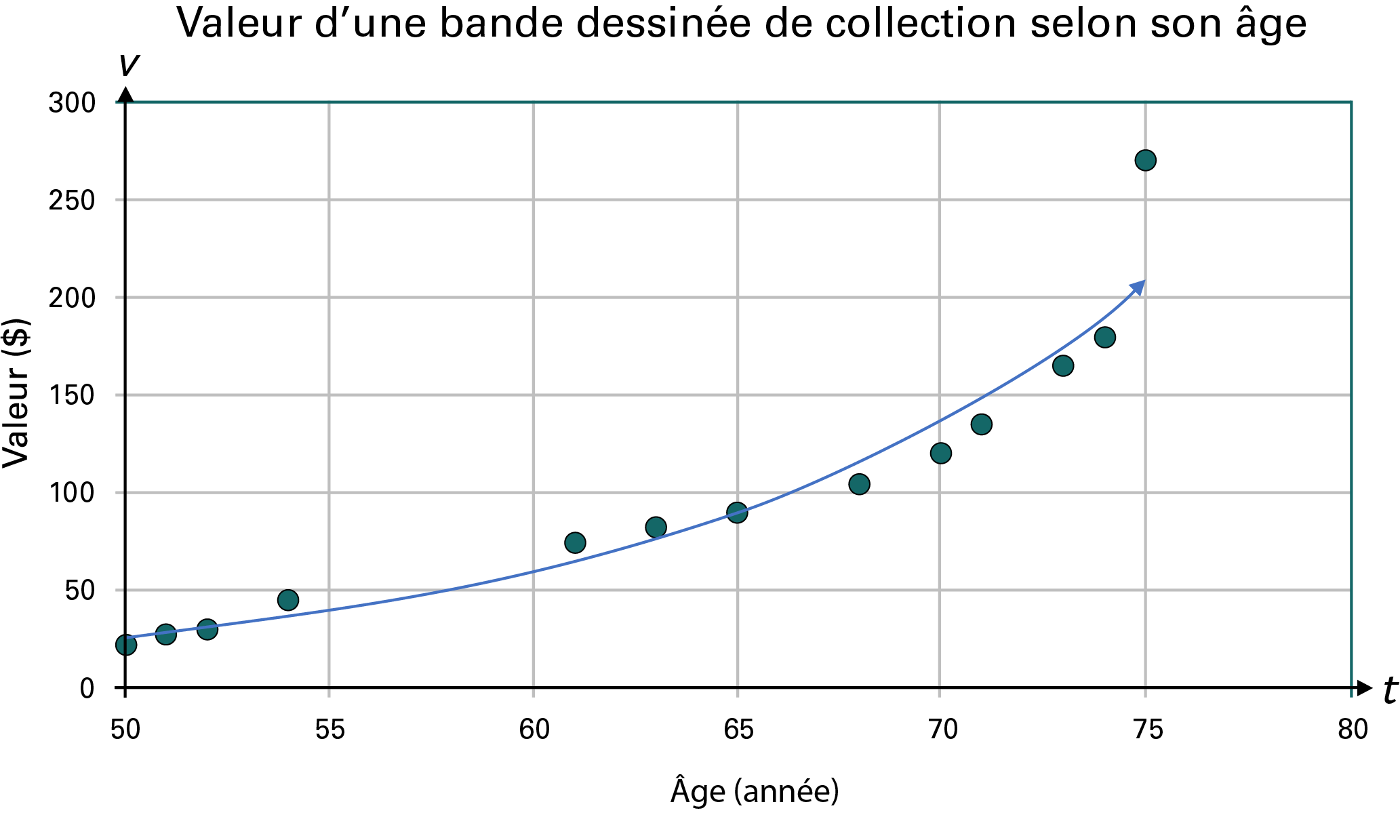
L’axe des ordonnées est de zéro à 300 par bonds de cinquante, il représente la valeur en dollars. L’axe des abscisses part de cinquante et va jusqu’à quatre-vingts par bonds de cinq, il représente l’âge en années. Les points forment une courbe régulière et croissante. Le dernier point est placé le plus haut à 75 ans la valeur sera de 275 dollars.
Ty reçoit cette bande dessinée en cadeau alors qu’elle a été publiée il y a 60 ans. Ty prévoit attendre que sa valeur ait au moins doublée avant de la revendre. Combien d’années environ doit-il attendre? Comment le sais-tu?
Géométrie et mesure : Nouvelles dimensions
Contenus d’apprentissage : E1.4, E1.5, F1.4
Processus mathématiques : Représentation, Résolution de problèmes
Le terrain de camping BeauSéjour possède 9 trous de mini-golf. Les propriétaires planifient reproduire les mêmes trous pour les enfants, mais en utilisant des longueurs qui font la moitié des trous originaux et en conservant les mêmes largeurs que ces derniers. Comme les trous seront deux fois moins longs, les propriétaires planifient que les coûts seront également diminués de moitié.
- En utilisant cet exemple de trous, détermine si les propriétaires ont tort ou raison.

Le contour du rectangle est brun. Une ligne brune est tracée de la gauche vers la droite en partant du centre du côté, mais ne va pas d’un bout à l’autre du rectangle. Un rond blanc est placé sous cette ligne à la gauche du rectangle. La longueur du rectangle est de trois mètres cinquante, et la largeur quatre-vingt-cinq centimètres.
- Élabore un budget démontrant les différences de coûts.
Tâche multidomaines
Contenus d’apprentissage : B3.5, D2.3, D2.4, D2.5, E1.3, F1.3
Processus mathématiques : Sélection d’outils et de stratégies, Raisonnement et justification, Réflexion, Communication, Représentation
Une famille veut installer des panneaux solaires sur le toit de sa maison pour réduire sa facture d’électricité et contribuer à la protection de l’environnement. Elle souhaite comprendre les coûts initiaux, les économies potentielles sur sa facture d’électricité et le temps nécessaire pour rentabiliser son investissement dans le but de déterminer si l’installation de panneaux solaires est le meilleur choix pour elle.
Voici un exemple d’un panneau solaire composé de six modules.

Voici quelques informations supplémentaires :
- La surface du toit propice à l’installation de panneaux solaires est de 400 pieds carrées (40 pi sur 10 pi).
- Les dimensions d’un module sont de 1 mètre sur 1,7 mètre. À Toronto, un module produit environ 395 kWh par an.
- Les coûts, en Ontario, en 2024 sont d’environ 2,50 $ par kWh. Mais, plus on en achète, plus les coûts diminuent.
- Établir les coûts : À l’aide des informations fournies ou de données fiables prises de l’Internet, détermine les coûts d’installation approximatifs de panneaux solaires.
- Établir un modèle : Détermine le coût moyen annuel d’électricité, soit en utilisant des données fiables sur l’Internet ou les informations provenant de ta propre famille, puis établit un modèle comparant les coûts annuels sans panneaux solaires et avec des panneaux solaires.
- Établir un objectif financier : La famille prévoit devoir emprunter une partie du montant pour réaliser le projet. Elle prévoit utiliser les économies faites en électricité pour rembourser le prêt. Si elle obtient un prêt à 4,5 % d’intérêt composé annuellement, combien d’années aura-t-elle besoin pour rembourser le prêt? Combien d’argent supplémentaire devrait-elle débourser si elle veut diminuer la durée du prêt de 5 ans?
Réflexion
- Quels sont les avantages et les défis de l’intégration de la littératie financière pour illustrer et appliquer les concepts des autres domaines du programme-cadre? Comment cette intégration peut-elle enrichir l’apprentissage des élèves, et quelles conséquences pratiques et pédagogiques pourrait-elle entraîner?
- En quoi l’intégration de la littératie financière à d’autres domaines d’études peut soutenir le développement de compétences transférables à l’aide de résolution de problèmes ayant des niveaux de complexité variés?
- Quels changements pourrait-on apporter aux problèmes offerts pour qu’ils soient plus pertinents et significatifs pour les élèves?
