Geometry and Measurement : Measurement
Connections Across Grades
Two-dimensional shapes
Specific Expectation: E2.4
Mathematical Processes: Problem Solving, Selecting Tools and Strategies
Lucas wants to plant a mix of flowers and vegetables in his garden.
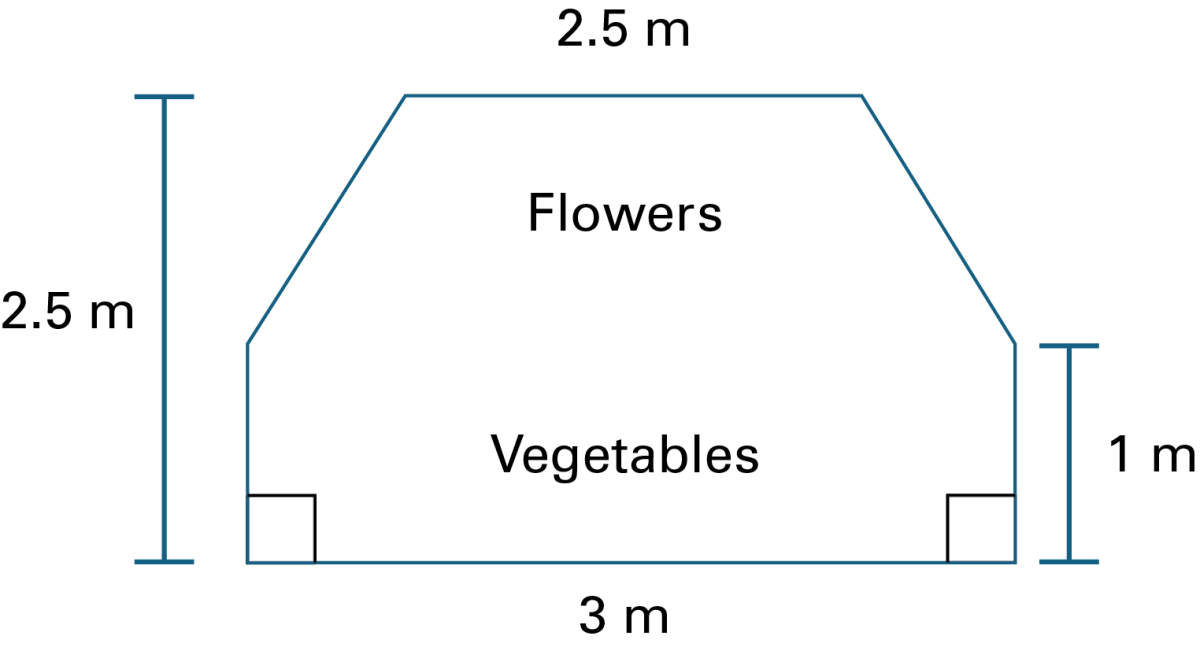
The height of the hexagon is 2 meters fifty. The measurement of the base is 3 meters. The sides perpendicular to the base are 1 meter. The side parallel to the base is 2 meters fifty. The word « vegetables » is written above the base and a bit higher the word « flower ».
Calculate the total area of the garden to determine the size of the tarp needed to cover it during the winter.
Specific Expectations: E2.2, E2.3, E2.7
Mathematical Processes: Problem Solving, Selecting Tools and Strategies
Marie wants to create a vegetable patch in her garden, using a rectangular section for vegetables and a circular section for aromatic herbs.

The semicircle is to the right of the rectangle. Inside the rectangle, there is the word « vegetables » and the word « aromatic herbs » is inside the semicircle. The total length of the shape is 3 meters fifty. Its height is 2 meters sixty.
- How much wire mesh is needed to enclose the garden?
- How many cubic metres of soil will Marie need for her vegetable garden if she has to add 10 cm of soil?
- How much mulch is needed to cover the soil of the aromatic herbs section?
Specific Expectations: E2.3, E2.4
Mathematical Processes: Problem Solving, Selecting Tools and Strategies
Kim wants to plant a vegetable garden. The garden must be fenced off to prevent animals from eating the vegetables.
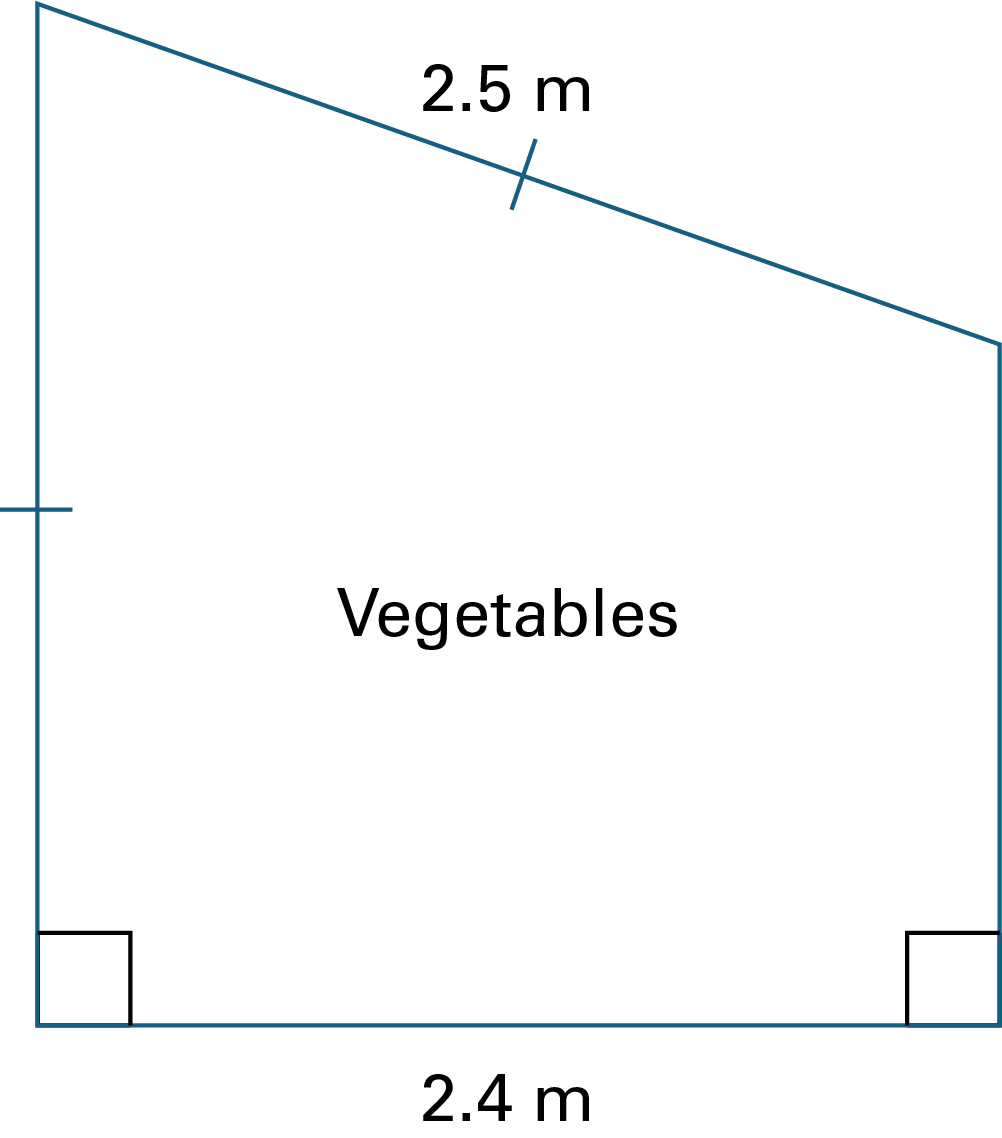
The base has two right angles and measures 2.4 metres. Above, the slanting side measures 2.5 metres.
How many metres of fence does Kim need?
Specific Expectation: E1.4
Mathematical Processes: Problem Solving, Reasoning and Proving, Reflecting, Representing, Selecting Tools and Strategies
In a rectangular garden, 10 metres long and 8 metres wide, an owner wishes to extend his planting area by increasing the length and width by the same number of metres.
- Using technological and digital tools such as 3D modeling software, determine the effect on the garden’s area if the owner decides to increase both the length and width by 3 metres.
- Using the same tools, determine how increasing the length and width of the garden affects its perimeter.
- Based on your results, demonstrate how simultaneous modification of the dimensions of a two-dimensional shape such as a rectangular garden affects both its area and its perimeter.
- Propose a general mathematical method for calculating the variation in area and perimeter of a rectangle when its dimensions are proportionally modified.
Three-dimensional objects
Specific Expectation: E2.1
Mathematical Processes: Problem Solving, Selecting Tools and Strategies
In daily life, it is often necessary to measure various objects or quantities to determine their volume or capacity.
- Describe a real-life situation where it would be more appropriate to use a small unit of measurement, a medium unit of measurement, or a large unit of measurement to determine the capacity. Specify the unit of measurement used.
- Explain why this unit of measurement would be more appropriate in each situation.
Specific Expectation: E2.7
Mathematical Processes: Problem Solving, Selecting Tools and Strategies
Sarah wants to build a small circular pond in her garden to raise fish. She plans to use a large plastic cylinder with a diameter of 2.4 metres and a depth of 1.6 metres as a reservoir.
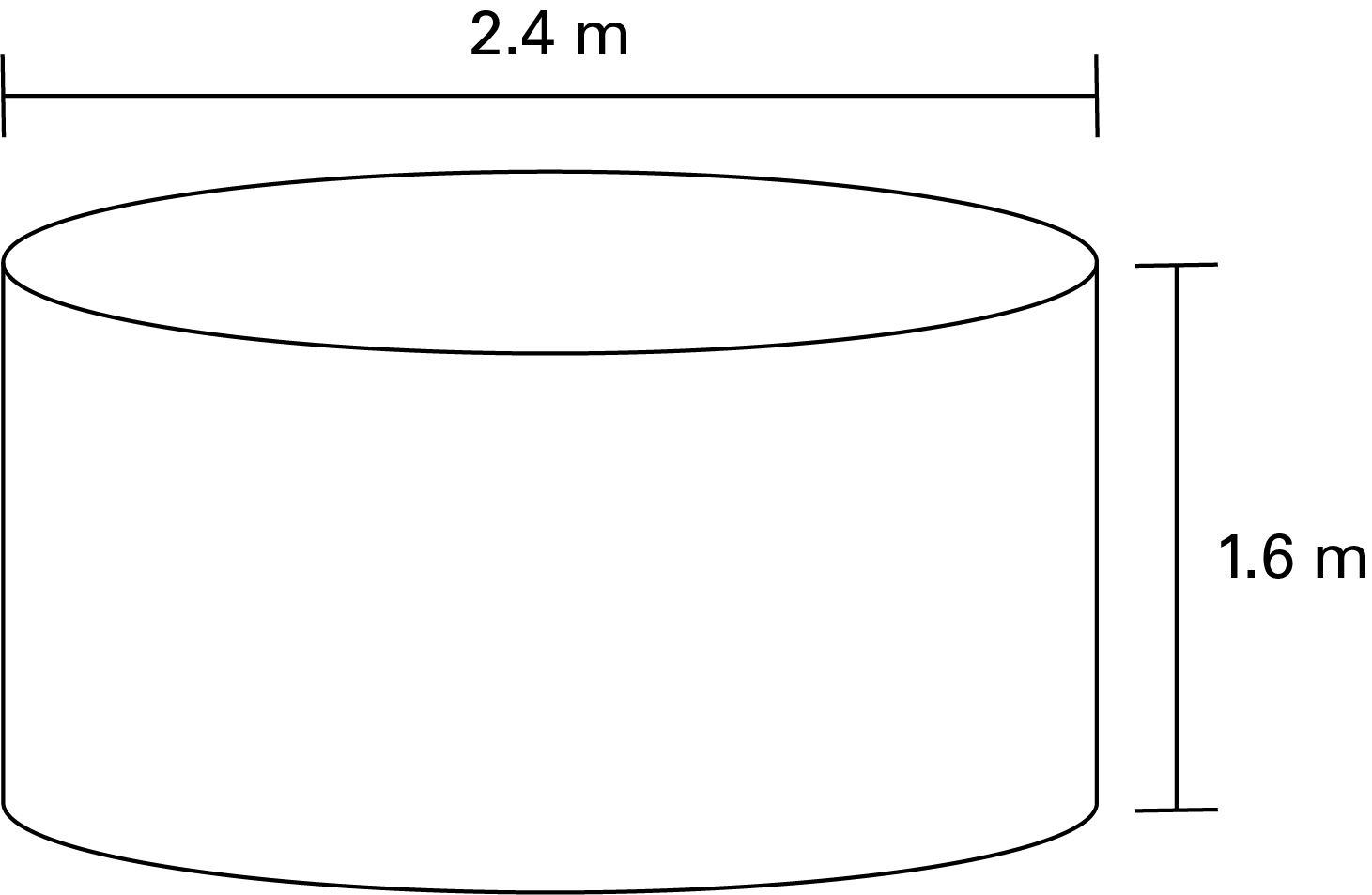
If Sarah wants to fill the cylinder to 80% of its capacity, how many litres of water will she need?
Specific Expectation: E2.3
Mathematical Processes: Problem solving, Reflecting
Design a lunchbox consisting of a prism and a half-cylinder with a capacity of between 1.5 and 2 L (1 L = 1000 cm3).
Specific Expectation: E1.4
Mathematical Processes: Problem solving, Reflecting
Noah has a rectangular prism-shaped wooden box for his valuables. He wants to make a new box twice the volume of the original. How should he adjust the dimensions of the new box in relation to his current one?
Reflection
- How can the diversity of two-dimensional shapes and three-dimensional objects in our environment be utilized to engage students in authentic and enriching tasks?
- How might you collaborate with a colleague to plan an interdisciplinary project for your students?
