Skip to content
Back to Strands
Français English
Back to Strands
Français English

Geometry and Measurement : Measurement

Connections With Other Strands

Our environment is filled with objects composed of basic geometric shapes. By having the opportunity to solve problems based on real-life situations from our surroundings, students see mathematics as an integral part of their daily lives. This type of problem helps students understand that all areas of mathematics are interconnected and form a cohesive whole.

The following examples demonstrate how concepts from various mathematical strands can be integrated into the study of the geometry and measurement strand.

When examining each question, reflect on the knowledge and skills from the overall and specific expectations in the Geometry and Measurement strand that students will use, as well as the connections to the key concepts.

​Number: Ratio

Specific Expectations: B3.5, E1.5
Mathematical Processes: Problem Solving, Selecting Tools and Strategies, Connecting

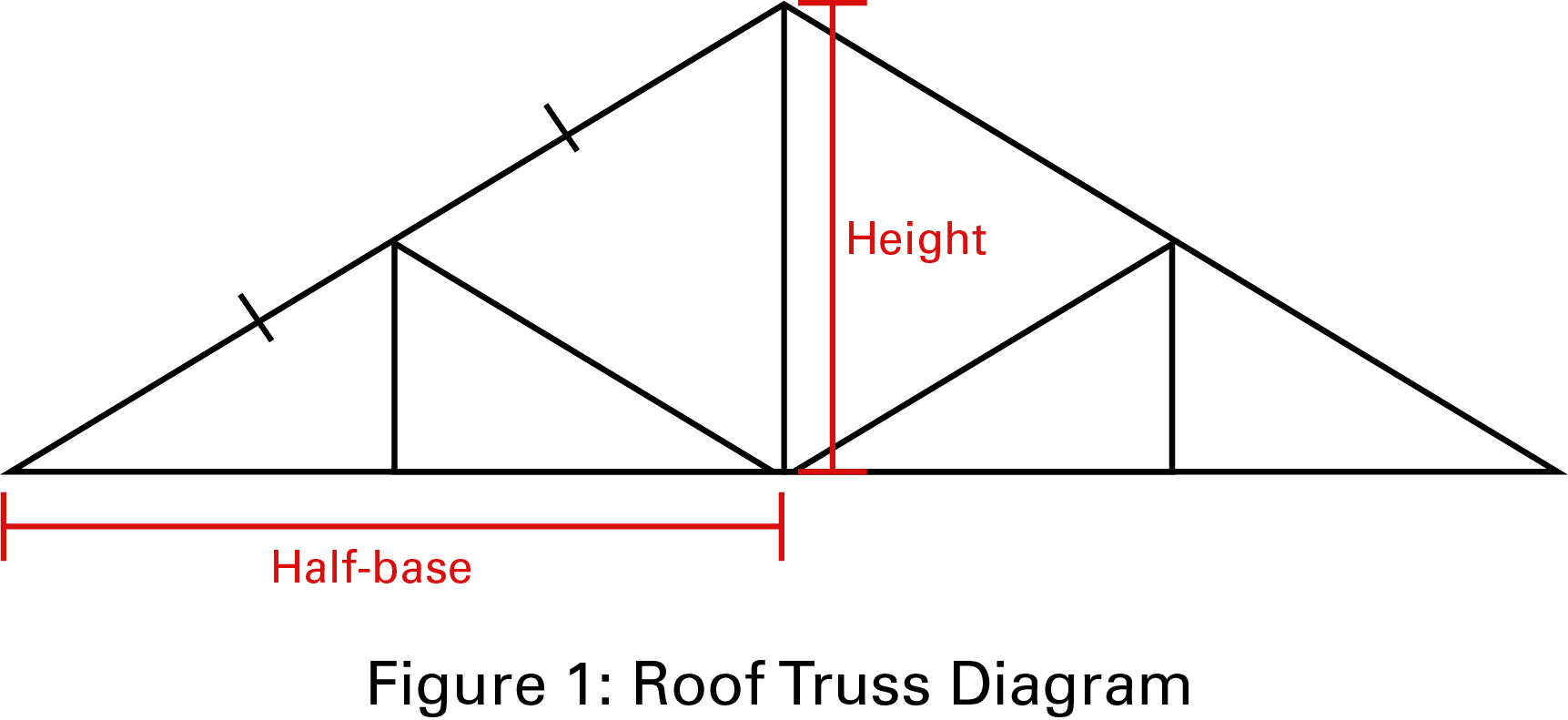
You need to build a roof truss with a slope ratio of 5:12 between the height and the half-base for a shed. ​​ Figure 1: Roof truss diagram.

Large isosceles triangle divided into several smaller triangles by 5 lines. A vertical line in the middle divides it into two identical rectangular triangles and represents the height. Under the one on the left, it says "half-base". Each half is divided into three triangles in the same way: there are two identical right-angled triangles and one equilateral triangle.

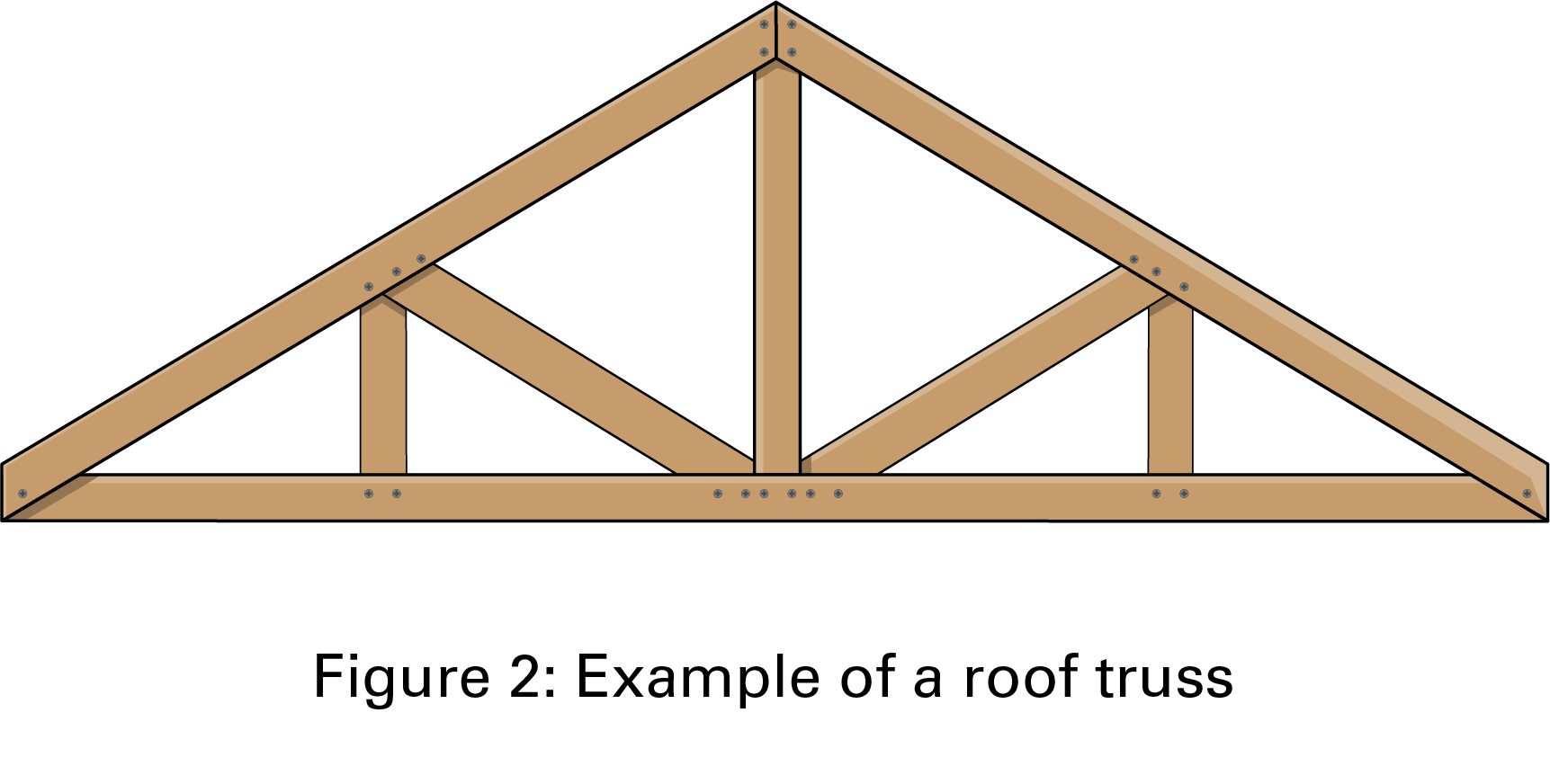
Figure 2 : Example of a roof truss. The entire structure in the previous diagram is illustrated by wooden beams.

Each roof truss must have a base length of 18 feet.

  1. Determine the total length of 2 by 6 inch wooden studs needed to construct one roof truss.
  2. The studs for constructing the roof truss are sold in lengths of either 8, 12 or 20 feet. How many boards of each stud should you purchase if you need to install roof trusses every 16 inches on a roof that is 12 feet long? Remember to account for waste since each piece of wood must be cut at an angle.

Algebra: Linear and Non-Linear Relations

Specific Expectations: C3.1, C4.1, E1.4
Mathematical Processes: Problem Solving, Representing

Imagine a cylinder with a radius of 0.1 cm and a height of 0.1 cm, having a volume of 0.001π cm3.

  1. Imagine that you double its height and determine its volume. You double the height again and determine the volume. You repeat this process several times.​ Four cylinders are placed in ascending order. Using a table of values and a graph, represent the volume of the cylinder as a function of its height when you double it each time while keeping the radius at 0.1 cm.
  2. Now, repeat the same exercise, but double the radius instead of the height. 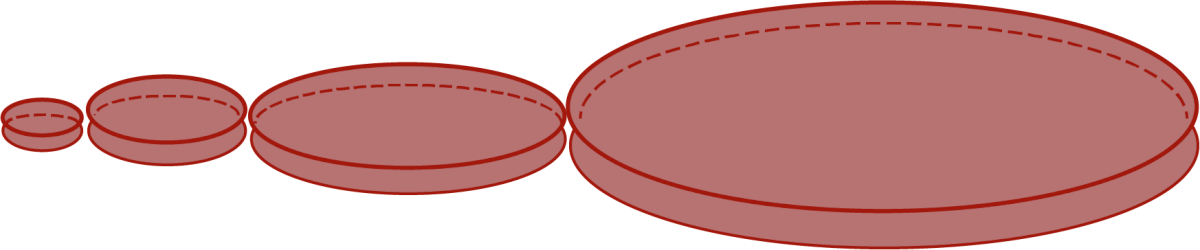Four cylinders with a small height and a large radius. The cylinders are in ascending order. Using a table values and a graph, represent the volume of the cylinder as a function of its radius when you double it each time while keeping the height at 0.1 cm.
  3. What are the differences and similarities between the two situations?
  4. What can you say about the volume of a cylinder when you double its height? its radius?

Data: Mathematical Model

Specific Expectations: D1.3, D2.4, E1.5
Mathematical Process: Problem Solving

Shrinkflation is a business strategy where the quantity of a product is reduced while the price remains the same. For example, an orange juice container that used to be 2 L has been reduced to 1.89 L. The difference is hardly noticeable to the human eye.

  1. Choose a product that comes in a cardboard package (for example, cereal, crackers, pasta).
  2. Find the dimensions of the container and the weight of the product.
  3. On average, companies reduce the weight by about 5% without the consumer noticing. Create a mathematical model showing the relationship between the reduction in the amount of packaging needed and the reduction in the weight of the product to produce 100 000 packages.

​Financial Literacy: Borrowing

​

Specific Expectations: E1.6, F1.3
​​Mathematical Processes: Representing, Problem Solving

​​​The GoodGrain farm needs to replace its grain silos. Here’s the type of silos ​​wanted. The cylindrical part is built by stacking rings of 2 feet and 2 inches each.

Here is the known information:

​​​Diameter: 18 feet

Number of rings of the cylindric part: 6

Each ring has a height of 2 feet and 2 inches.

Maximum capacity of the cylindric part (where the grain is stored): 85 m3

Cost: $26,000 ($5,000 for the roof, $3,500 per ring)

Possible Options:

  1. The owners wish to store approximately 375 m³ of grain. Other possible dimensions for the silo are:
    • 1.5 times the diameter
    • 1.5 times the number of rings
    • 2 times the diameter
    • 2 times the number of rings

They can choose two options but cannot double both dimensions at the same time. What would you recommend they purchase and why?

Cost: Starting with the basic model, for every increase of 3 feet in diameter, the cost of the roof increases by $500, and the cost of the rings increases by $525.

  1. Determine the cost of the silo you recommended. Should your recommendation change? Explain your answer.
  2. The financial institution has approved a loan of $50,000 at an interest rate of 4.5% per year to help with this purchase. The owners have saved $30,000 that can be used for this purchase. They need to make decisions about certain elements of the loan:
    • How much should they borrow? Should they use part or all their savings to reduce the amount borrowed?
    • What should be the term of their loan: 15, 20, or 25 years?
    • Should they make monthly or bi-weekly payments?

What recommendations would you give them?

Explain your choices using data.

Multi-Strand Task

Specific Expectations: B3.5, D2.4, D2.5, E1.3, F1.4
Mathematical Processes: Selecting Tools and Strategies, Reasoning and Proving, Reflecting, Communicating, Representing​​

As part of their class project, students must design and construct a model of a world​-​famous monument. ​They have chosen to reproduce the​ Great Pyramid of Giza in Egypt. However, the students face a problem: the actual dimensions of the ​​ Great Pyramid of Giza are given in metric units, while the materials used to build the model are measured in imperial units.

  1. The height of the Great Pyramid of Giza is 138.8 metres. The base of the pyramid is a square with each side measuring 230.4 metres. Convert these measurements into compatible units to determine the quantity of material needed. ​​
  2. Create a scale plan of the model. The total height of the model must not exceed 2 feet. Students can use technological and digital tools, such as 3D modeling software, to represent the scale model of the Great Pyramid.
  3. Students conduct research to determine the available construction materials (for example, corrugated cardboard, Balsa wood) and their costs. Using various representations such as tables, diagrams, tables of values, or graphs, students compare the costs of materials to build their model. ​
  4. Students present a budget to justify their choice of dimensions based on the materials they selected.

Reflection

  • How can we integrate and assess learning expectations from various strands through the use of measurement problems?
  • How can we encourage students to recognize and reflect on how their understanding of numbers and algebra is important to their study of measurement and when solving measurement problems?
  • What adjustments can I make to my teaching strategies to help students persist in deepening their conceptual understanding of mathematics through solving rich and authentic problems?