Algèbre : Expressions, équations et inéquations
Concepts clés
Les expressions algébriques
- Les expressions algébriques sont utiles, entre autres, pour généraliser des situations variées, telles que les suites numériques et les suites à motif.
- Il existe une infinité d’expressions algébriques équivalentes.
- Une même situation peut être représentée par plusieurs expressions algébriques équivalentes, mais chacune montre un raisonnement différent.
- Une expression algébrique est composée de constantes et de variables reliées par des symboles d’opérations mathématiques. Elle ne comprend ni signe d’égalité, ni signe d’inégalité (par exemple, \(n\left(n-1\right)+4\), \(\frac{-7}{x}+{1{,}5}\) ). Chaque élément séparé par une addition ou une soustraction est un terme.
- Un coefficient est un multiplicateur placé devant la ou les variables d’un terme.
- Les termes semblables diffèrent entre eux uniquement par leur coefficient (par exemple, \(3ab^2\) et \(-ab^2\), \(-\frac{3}{4}x\) et \(x\) ). Ils peuvent être additionnés et soustraits.
- Un monôme est composé soit d’un nombre (constante) ou du produit d’un coefficient et de variables dont les exposants sont des nombres naturels (par exemple, \(4,\ 3x,\ \frac{3b}{4},\ 4p^3rt^2\)).
- Les polynômes sont un type particulier d’expressions algébriques représentés par la somme algébrique de plusieurs termes, qui sont exclusivement des monômes. Un binôme est la somme de deux monômes (par exemple, \(3{,}5x-5{,}2\)) et un trinôme, la somme de trois monômes (par exemple, \(4x^2+12x-5\)).
Le tableau suivant résume le développement de la compréhension des expressions algébriques, au cours des années d’études.
| Année d’études | Connaissances et habiletés | Types de nombres |
|---|---|---|
| 4e | Utiliser des symboles (images et lettres) comme variables dans des expressions algébriques | |
| 5e | Décrire des relations d’équivalence | |
| Évaluer des expressions algébriques | Nombres naturels | |
| 6e | Additionner des monômes (1er degré) | Nombres naturels |
| Évaluer des expressions algébriques | Nombres naturels et nombres décimaux (dixièmes) | |
| 7e | Additionner et soustraire des monômes (1er degré) | Nombres naturels |
| Évaluer des expressions algébriques | Nombres naturels et nombres décimaux | |
| 8e |
Additionner et soustraire des monômes (1er degré) Additionner des binômes (1er degré) |
Nombres entiers |
| Évaluer des expressions algébriques | Nombres rationnels | |
| 9e | Créer, comparer et simplifier des expressions algébriques | Nombres réels |
Les équations
- Une équation est un énoncé mathématique comportant une ou plusieurs variables et un symbole d’égalité. Elle exprime une égalité entre deux expressions algébriques.
- Certaines équations ont un nombre fini de solutions, alors que d’autres ont une infinité de solutions ou aucune solution.
- Une équation à résoudre comporte une seule variable, appelée inconnue, et la solution est la ou les valeurs de l’inconnue qui rendent l’égalité vraie. Elle peut avoir :
- un nombre fini de solutions (par exemple, \(3\left(4x-5\right)=8x+11\), \(\frac{2}{3}x+\frac{3}{5}=\frac{5}{6}x-\frac{4}{5}\));
- un nombre infini de solutions (par exemple, \(2x+4=2\left(x+2\right)\));
- aucune solution (par exemple, \(2x+4=2x+5\ \)).
- Une équation peut exprimer la relation qui existe entre deux variables. Il peut exister une infinité de valeurs pour les deux variables, tant que la relation est maintenue (par exemple, \(C=12h+35\), \(y=-3x+12\), \(x+y=24\)).
- Une formule est une expression générale qui comporte plusieurs variables et qui décrit une relation qui est toujours vraie (par exemple, \(V=\frac{1}{3}\pi r^2h\), \(F=\frac{9}{5}C+32\)).
- Une équation peut exprimer l’égalité entre deux expressions algébriques équivalentes. Cette égalité est toujours vraie, peu importe la valeur de la variable (par exemple, \(3x+5x=8x,\) \(2x\left(3x-5\right)=6x^2-10x\) ).
- Une équation à résoudre comporte une seule variable, appelée inconnue, et la solution est la ou les valeurs de l’inconnue qui rendent l’égalité vraie. Elle peut avoir :
- Une variété de représentations, de stratégies ou d’outils peuvent être utilisés pour résoudre une équation. Certains d’entre eux sont plus appropriés selon le contexte ou le type d’équation.
Le tableau suivant résume les types de nombres utilisés ainsi que le niveau de complexité des équations à résoudre pour chaque année d’études.
| Année d’études | Types d’équations | Types de nombres |
|---|---|---|
| 4e | \begin{align}12 + a + 7 &= 32 + 17 \\ 40 − 15 &= 2 \times n − 5\end{align} | Nombres naturels jusqu’à 50 |
| 5e | \begin{align}52 + a + 27 &= 72 + 17 \\ 80 − 24 &= 2n − 48\end{align} | Nombres naturels jusqu’à 100 |
| 6e | \begin{align}80 − 24 &= 2n + 4n \\ 5a + 2a &= 109 − 25\end{align} | Nombres naturels |
| 7e | \begin{align}3m + 5m &= 98 + 62 \\ 4,5p + 2,3p &= 14,7 + 12,5\end{align} | Nombres naturels et nombres décimaux |
| 8e | \begin{align}−5x − 7x &= −40 − (−4) \\ 4,5p − 12,7 &= 2,3p + 4,9 \\ 132 &= x^2 + 122\end{align} | Nombres entiers et nombres décimaux |
| 9e | \begin{align}3n + 42 &= −15 \\ −3(3x + 4) &= 7(−x − 5) \\ 23r − 4 &= 5r + 35\end{align} | Nombres rationnels |
Les inéquations
- Les inéquations sont des énoncés mathématiques comportant un des symboles d’inégalité.
- \(<\) se lit est inférieur à…
- \(>\) se lit est supérieur à…
- \(\leq\) se lit est inférieur ou égal à…
- \(\geq\) se lit est supérieur ou égal à…
- La solution d’une inéquation du type a\(x\) + b\(y\) > k peut être représentée par une région ombrée dans un plan cartésien dont la droite de l’équation correspondante a\(x\) + b\(y\) = k est la limite. Si la droite fait partie de l’ensemble solution, celle-ci serait pleine, si elle n’en fait pas partie, elle sera pointillée.
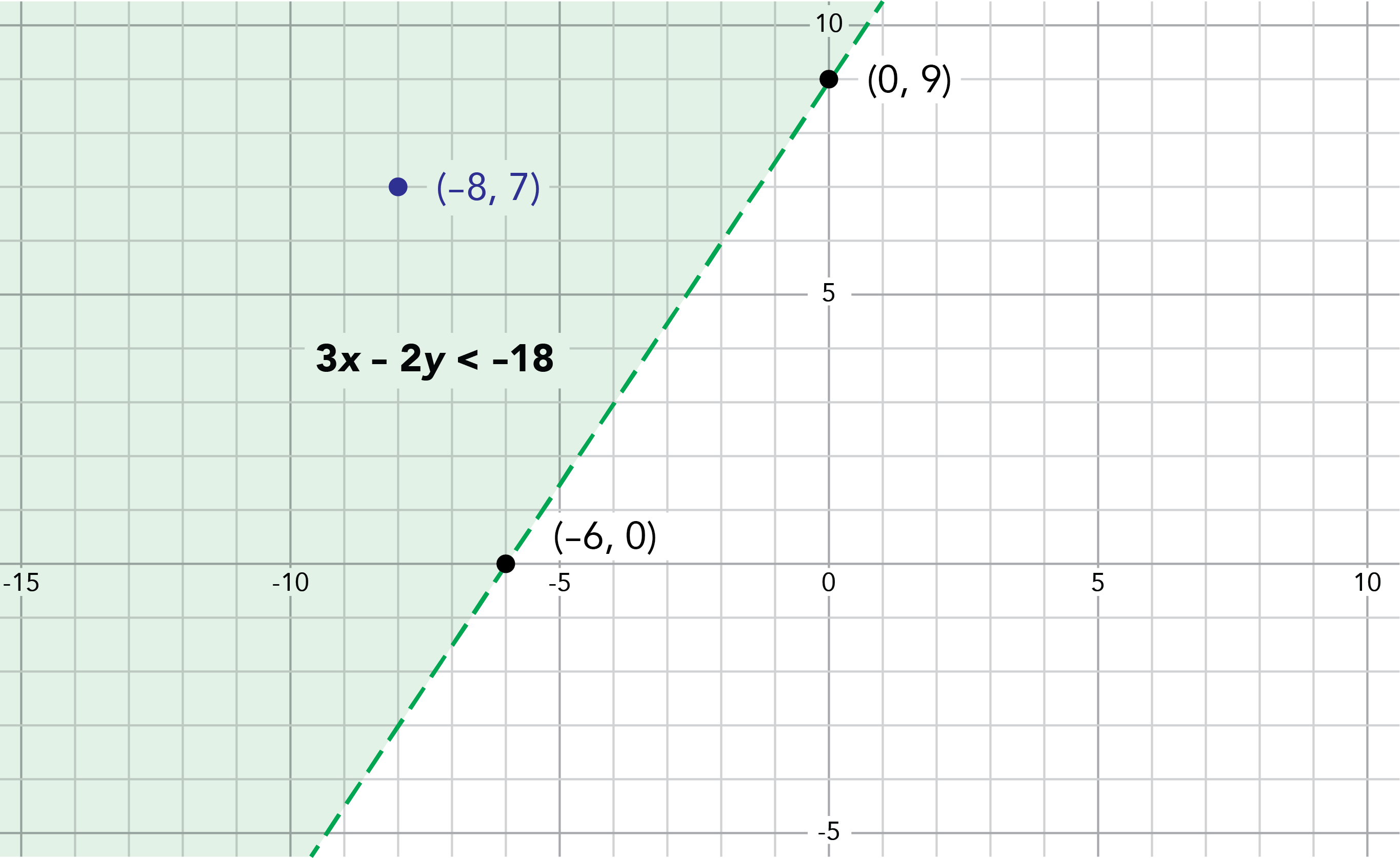
Sur le plan cartésien numéroté par intervalles de 5, la droite pointillée traverse les coordonnées moins 6, 0 ainsi que 0, 9. Dans la zone ombrée, il est écrit « 3x moins 2y est plus petit que moins 18 ». Un point situe la coordonnée moins 8, 7.
- Il est possible de déterminer l’ensemble solution de l’inéquation en substituant l’ordonnée et l’abscisse d’un point dans l’inéquation (par exemple, le point (–8, 7)). Si les coordonnées du point rendent l’inégalité vraie, le point fait partie de l’ensemble solution et fera partie de la région ombrée du plan.
- La résolution d’inéquations sert à modéliser et à résoudre des problèmes et des situations du monde réel où les valeurs peuvent varier dans un certain intervalle ou doivent respecter certaines limites.
Le tableau suivant résume les types de nombres utilisés ainsi que le niveau de complexité des inéquations à résoudre pour chaque année d’études à partir de la 4e année, où les inéquations sont introduites.
| Année d’études | Types d’inéquations | Types de nombres |
|---|---|---|
| 4e | \begin{align}a + 12 &≤ 20 \\ 18 − b &> 7\end{align} | Nombres naturels jusqu’à 20 |
| 5e | \begin{align}n + 3 &< 9 \\ 3m &≥ 18\end{align} | Nombres naturels jusqu’à 50 |
| 6e | \begin{align}3m − 8 &≥ 19 \\ 20 &< \frac{a}{3} + 7\end{align} | Nombres naturels jusqu’à 100 |
| 7e | \begin{align}12c − 7c &≤ 13 + 27 \\ 35 + 29 &> 5x + 11x\end{align} | Nombres naturels |
| 8e | \begin{align}−2p − 6p &< 17 + 15 \\ 5x − 12 &≥ 3x + 8\end{align} | Nombres entiers |
| 9e | \begin{align}−3y &< 27 \\ 2x + 3y &≥ 48\end{align} | Nombres rationnels |
Réflexion
- En quoi une compréhension approfondie des opérations avec des nombres influence-t-elle la capacité à manipuler des expressions algébriques et à résoudre des équations?
- Quel rôle joue le développement du raisonnement algébrique dans la compréhension des opérations avec des expressions algébriques et des équations?
- En quoi la compréhension approfondie des équations enrichit-elle l’approche et l’efficacité des élèves dans la résolution des inéquations?
- Comment les inéquations modélisent-elles des situations réelles différemment des équations, et quel impact cela a-t-il sur la prise de décision et la résolution de problèmes?
