Algèbre : Expressions, équations et inéquations

Outils et stratégies pédagogiques

« Traditionnellement, l’algèbre a souvent été présentée au secondaire comme une syntaxe prédéterminée de règles et un langage symbolique devant être mémorisé par les élèves. On s’attendait à ce que les élèves maîtrisent la manipulation symbolique avant d’apprendre quels étaient le but et l’utilisation des symboles. Autrement dit, on a présenté l’algèbre aux élèves en leur donnant peu de possibilités de l’explorer ou d’y trouver un sens. Toutefois, le curriculum de mathématiques de l’Ontario stipule qu’il faut proposer aux élèves une gamme de possibilités d’exploration et de recherche de sens. » (Ministère de l’Éducation de l’Ontario, 2013, Mettre l’accent sur le raisonnement algébrique, p. 8). En encourageant les élèves à utiliser et à comparer une variété de stratégies et d’outils, le personnel enseignant les aide à développer une compréhension conceptuelle de l’algèbre.

Les expressions algébriques

Pour simplifier des expressions algébriques, les élèves doivent faire appel à leur compréhension des opérations sur les nombres rationnels ainsi que sur les exposants. L’utilisation de matériel de manipulation vise à développer une compréhension conceptuelle des opérations sur les expressions algébriques. Toutes et tous les élèves devraient être encouragés à démontrer leur compréhension à l’aide d’une variété de représentations incluant du matériel de manipulation.

Voici quelques outils et stratégies pratiques qui peuvent être utilisés pour simplifier des expressions algébriques.

Expression algébrique	Outils	Stratégies
Multiplication d’un monôme avec des monômes et des polynômes	Tuiles algébriques Disposition rectangulaire	Loi des exposants. Priorité des opérations. Distributivité.
Addition et soustraction de monômes	Tuiles algébriques	Regroupements des termes semblables (commutativité). Disposition verticale (telle que l’addition de nombres à plusieurs chiffres).

Les équations

Les équations algébriques sont utilisées pour représenter une variété de situations et de contextes. La compréhension et l’établissement de liens entre les différents types d’équations par les élèves les aide à sélectionner des stratégies et des outils appropriés et efficaces dans la résolution de problèmes impliquant des équations.

Voici quelques exemples d’équations, d’outils et de stratégies possibles selon le type d’équations.

Type d’équation	Exemples	Outils	Stratégies
Une identité algébrique (toujours vraie)	\begin{align}3x + 5x &= 8x \\ 2x(3x − 5) &= 6x^2 − 10x\end{align}	Tuiles algébriques Disposition rectangulaire	Substituer une valeur numérique. Simplifier et comparer des expressions algébriques.
Relation entre deux variables (dépendante et indépendante)	\begin{align}C &= 12h + 35 \\ y &= −3x + 12 \\ x + y &= 24\end{align}	Diagrammes (nuage de points, graphique) Table de valeurs Situation en mots Représentation visuelle concrète ou semi-concrète (par exemple : tuiles algébriques, tuiles carrées, application de calculatrice graphique en ligne) Codage	Établir des liens entre plusieurs outils de représentation afin de développer la compréhension des relations entre deux variables.
Formules	\begin{align}V &= πr^3 \\ A &= 2πr^2 + 2πrh\end{align}	Solides et leur développement Logiciels de géométrie 2D et 3D Codage	Substituer des valeurs numériques. Explorer les relations entre différents solides.
Équation à résoudre	\begin{align}3(4x − 5) &= 8x + 11 \\ 23x + 35 &= 56x − 45\end{align}	Tuiles algébriques Droite ouverte double Tableau de proportionnalité Codage	Appliquer le principe de la balance. Transformer l’équation avec des fractions équivalentes.

Exemple de résolution de \(\frac{2}{3}x+\frac{3}{5}=\frac{5}{6}x-\frac{4}{5}\) à l’aide d’une droite ouverte double

Explication	Représentation visuelle	Représentation symbolique
Comme les deux membres de l’équation sont égaux, ils se trouvent au même endroit sur la droite numérique.	Un trait vertical, donne un point. Au-dessus de ce point il y a une équation : 2 troisièmes « x » plus 3 cinquièmes En-dessous de la ligne verticale, il y a une autre équation : 5 sixièmes « x » moins 4 cinquièmes.	\begin{align}\frac{2}{3}x+\frac{3}{5}=\frac{5}{6}x-\frac{4}{5}\end{align}
Je choisis de reculer de \(\frac{2}{3}x\) afin d’avoir une variable seulement en bas.	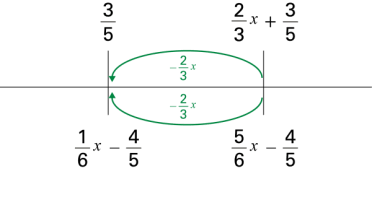Il y a deux traits verticaux placés sur cette droite, chaque trait représente une valeur spécifique sur la droite numérique. Au-dessus du premier qui est plus à droite, il y a l’équation suivante : 2 troisièmes « x » plus 3 cinquièmes. En dessous de ce trait il y a l’équation suivante : 5 sixièmes « x » moins 4 cinquièmes Le second trait est placé vers la gauche de la droite. Au-dessous de ce dernier, il y a la fraction suivante : 3 cinquièmes. En dessous du trait il y a l’équation suivante : Un sixième « x » moins 4 cinquièmes Entre les deux traits, il y a deux flèches vertes. Elles partent toutes deux du trait de droite et pointe vers le trait de gauche. La première est au-dessus de la droite et la seconde en dessous. Chacune des flèches est accompagnée de la fraction suivante : Négatif 2 troisièmes « x »	\begin{align}\frac{2}{3}x-\frac{2}{3}x+\frac{3}{5} &= \frac{5}{6}x-\frac{2}{3}x-\frac{4}{5} \\ \frac{3}{5} &= \frac{1}{6}x-\frac{4}{5}\end{align}
En observant les expressions sur la droite, je sais que lorsque j’enlève une quantité, ici j’enlève \(\frac{4}{5}\) à \(\frac{1}{6}x\) , je me déplace vers la gauche. Donc, je peux déduire que \(\frac{1}{6}x\) sera de \(\frac{4}{5}\) d’unité à la droite de \(\frac{1}{6}x - \frac{4}{5}\).	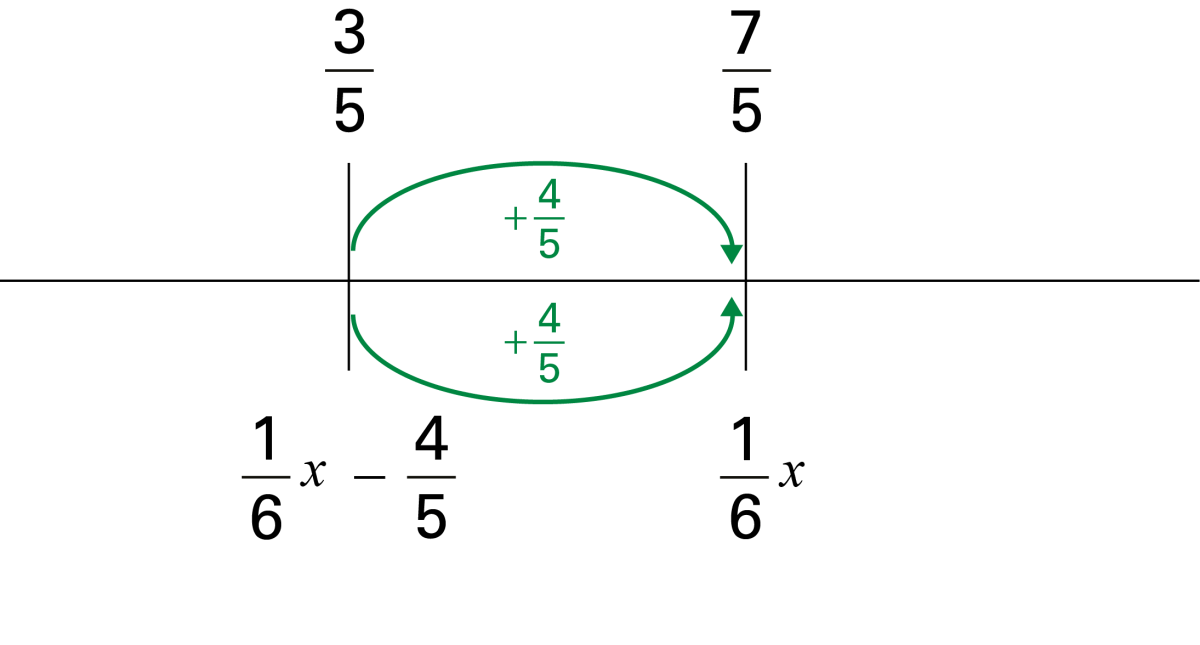Il y a deux traits verticaux placés sur la droite, chaque trait représente un point spécifique sur la droite numérique. Au-dessus du premier qui est plus à gauche, il y a la fraction suivante : 3 cinquièmes. En dessous de ce trait, il y a la fraction suivante : Un sixième « x » moins 44 cinquièmes Le second trait est placé vers la droite de la droite numérique. Au-dessus de ce dernier, il y a la fraction suivante : 7 cinquièmes. En dessous du trait il y a l’équation suivante : Un sixième « x » moins 4 cinquièmes Entre les deux traits, il y a deux flèches vertes. Elles partent toutes deux du trait de gauche et pointe vers le trait de droite. La première est au-dessus de la droite et la seconde en dessous. Chacune des flèches est accompagnée de la fraction suivante : Positif 4 cinquièmes	\begin{align}\frac{3}{5}+\frac{4}{5} &= \frac{1}{6}x-\frac{4}{5}+\frac{4}{5} \\ \frac{7}{5} &= \frac{1}{6}x\end{align}
Je peux faire six bonds de \(\frac{1}{6}x\) sur la droite numérique pour déterminer où se situe un \(x\). Je fais également six bonds de \(\frac{7}{5}\). J’arrive donc à \(\frac{42}{5}\) sur la droite numérique.	Chaque bond est exprimé par deux expressions différentes. Le premier bond part du point zéro. Premier point : 7 cinquièmes ou un sixième « x » Deuxième point : 14 cinquièmes ou 2 sixièmes « x » Troisième point : 21 cinquièmes ou 3 sixièmes « x » Quatrième point : 28 cinquièmes ou 4 sixièmes « x » Cinquième point : 35 cinquièmes ou 5 sixièmes « x » Sixième point : 42 cinquièmes ou 6 sixièmes « x »	\begin{align}\frac{7}{5}\times 6 &= \frac{1}{6}x\times 6 \\ \frac{42}{5} &= x\end{align}

La solution de cette équation est donc \(x=\frac{42}{5}\) ou \(8\frac{2}{5}\).

Note : L’élève aurait pu commencer par n’importe quel terme. Dans certains cas, il aurait alors été nécessaire d’utiliser la symétrie de la droite si le coefficient de \(x\) est négatif.

Une droite numérique est représentée, sur cette droite il y a 3 trois points.

Exemple de résolution de l’équation \(\frac{2}{3}x+\frac{3}{5}=\frac{5}{6}x-\frac{4}{5}\) à l’aide de fractions équivalentes

Explications	Représentation visuelle	Représentation symbolique
Je remarque que tous les termes de l’équation comportent des fractions.		\begin{align}\frac{2}{3}x+\frac{3}{5}=\frac{5}{6}x-\frac{4}{5}\end{align}
Je peux exprimer toutes les fractions avec des fractions équivalentes ayant un dénominateur de 30.		\begin{align}\frac{20}{30}x+\frac{18}{30}=\frac{25}{30}x-\frac{24}{30}\end{align}
Je peux multiplier chaque terme de l’équation par 30 pour créer des nombres entiers.		\begin{align} \frac{20}{30}x \times 30 + \frac{18}{30} \times 30 = \frac{25}{30}x \times 30 - \frac{24}{30} \times 30 \end{align}
Je peux utiliser des tuiles algébriques à partir de cette étape pour représenter l’équation puisque les coefficients sont de nombres entiers.	En premier il y a 4 groupes de 5 tuiles vertes « x » et 18 tuiles orange de, un. Puis à côté, il y a 5 groupes de tuiles vertes « x » et 18 tuiles blanches, négatif un.	\begin{align}20x+18=25x-24\end{align}
En utilisant le concept de l’égalité (ou des tuiles algébriques), je constate que je peux enlever \(20x\) de chaque côté.	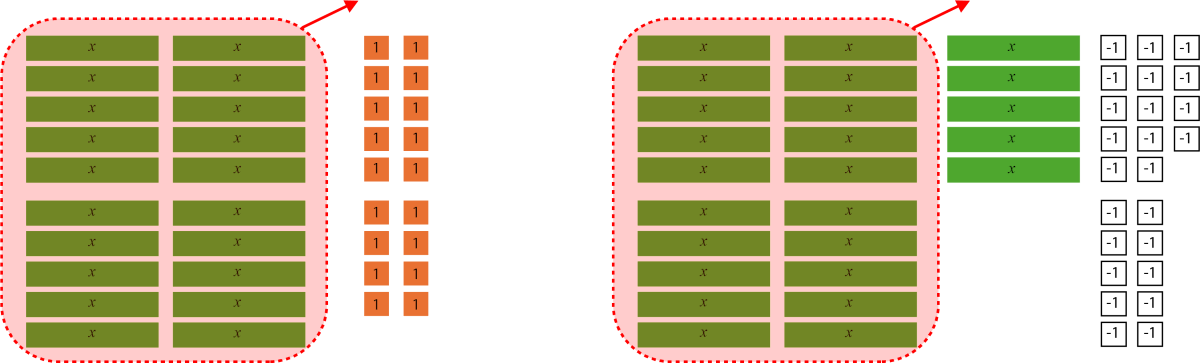En premier il y a 4 groupes de 5 tuiles vertes « x » et 18 tuiles orange de, un. Puis à côté, il y a 5 groupes de tuiles vertes « x » et 18 tuiles blanches, négatif un. De chaque côté, 20 tuiles de « x » sont encerclées en rouge et une flèche pointe vers le haut.	\begin{align}20x-20x+18 &= 25x-24-20x \\ 18 &= 5x-24\end{align}
Je peux également ajouter 24 de chaque côté afin de créer des paires nulles.	À la gauche, il y a 6 groupes de 5 tuiles orange et 3 groupes de 4 tuiles orange. À droite, il y a un groupe de 5 tuiles vertes et, encercler en rouge, 24 tuiles blanches de, négatif un et 24 tuiles orange de, un. Une flèche rouge part ce groupe qui est encerclé et pointe vers le haut.	\begin{align}18+24 &= 5x-24+24 \\ 42 &= 5x\end{align}
Je divise ensuite 42 en cinq groupes égaux afin de déterminer la valeur de \(1x\)	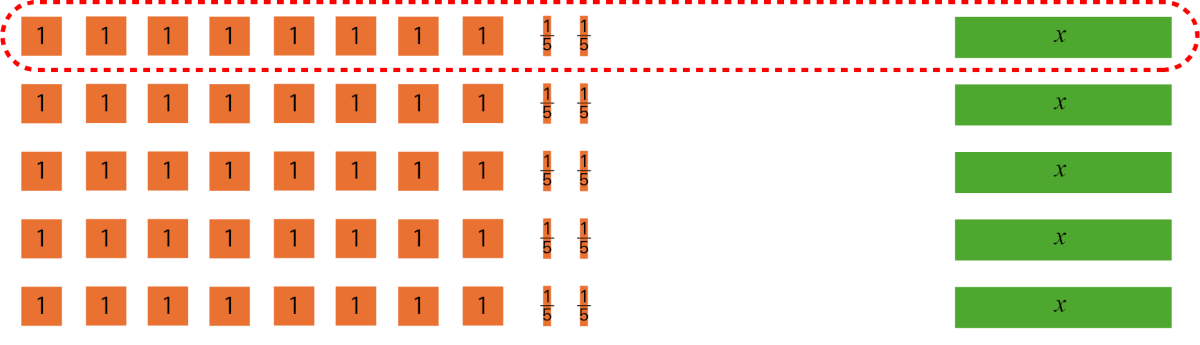Il y a 5 rangées de tuiles, elles sont identiques. 8 tuiles orange de, un, 2 tuiles orange de, un cinquième, et une tuile verte « x ». La première rangée est encerclée par un pointillé rouge.	\begin{align}42\div 5 &= 5x\div 5 \\ x &= \frac{42}{5}\ ou\ 8\frac{2}{5}\end{align}

La solution de cette équation est donc \(x=\frac{42}{5}\) ou \(8\frac{2}{5}\) ou 8,4.

Les inéquations

L’utilisation de la technologie et d’applications de représentation graphique dynamique aide les élèves à faire des conjectures en observant rapidement des régularités dans de nombreux exemples. Elles et ils seront ensuite en mesure de faire des généralisations à l’aide de ces outils.

En observant les quatre équations, les quatre graphiques et les coordonnées à l’origine, les élèves peuvent faire des conjectures et des généralisations liées aux coefficients et à la constante des équations avec les valeurs des coordonnées à l’origine.

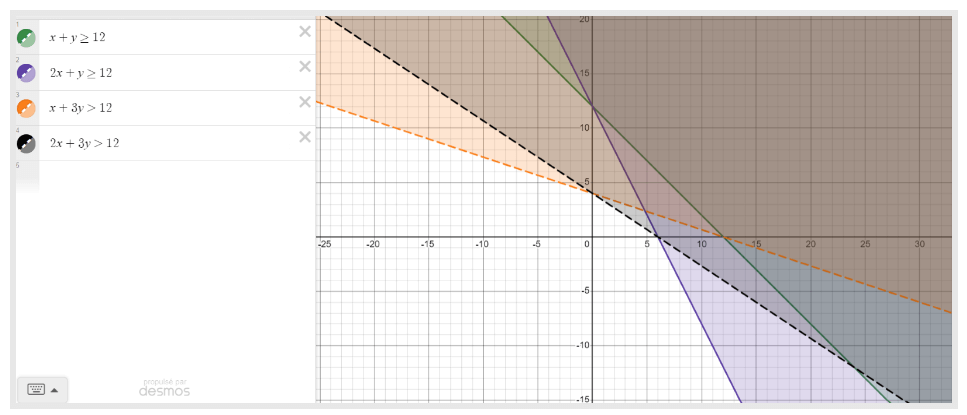
Plan cartésien numéroté par intervalles de 5, traversé de 4 droites.

Pour représenter l’ensemble solution de l’inéquation \(2x+3y\ge 12\), soit la région ombrée, les élèves peuvent d’abord résoudre l’équation équivalente \(2x+3y=12\) en utilisant les stratégies présentées dans la section précédente et représenter la droite. Cette droite représente la limite de l’ensemble solution. Les élèves peuvent ensuite choisir un point d’un côté ou de l’autre de la droite afin de déterminer si ce point fait partie de l’ensemble solution de l’inéquation. Si les coordonnées du point rendent l’inégalité vraie, le point fait partie de l’ensemble solution et fera partie de la région ombrée du plan.

Réflexion

Comment l’utilisation d’une variété de représentations concrètes, semi-concrètes, à l’aide de mots (à l’écrit ou à l’oral) ou en lien avec la vie quotidienne, permet-elle de développer la compréhension de l’algèbre afin que la représentation symbolique ait plus de sens pour l’élève?
En quoi la représentation graphique des équations et des inéquations peut-elle offrir une perspective supplémentaire dans leur résolution et leur interprétation?
Quels effets y aurait-il à rendre les diverses stratégies utilisées par les élèves visibles et disponibles à l’ensemble des élèves de la classe?
Comment peut-on encourager l’utilisation d’une stratégie autre que l’application mécanique d’un algorithme pour développer une compréhension approfondie des concepts algébriques chez les élèves?