Algèbre : Expressions, équations et inéquations
Liens entre les années d’études
L’évolution des contenus d’apprentissage d’algèbre d’une année d’études à l’autre aide les élèves à développer leur raisonnement algébrique et une compréhension conceptuelle des variables, des expressions algébriques, des équations et des inéquations.
Certaines différences notables résident dans le type de nombres ainsi que la complexité des expressions que les élèves doivent manipuler. Les exemples dans les tableaux suivants reflètent cette évolution.
Les expressions algébriques
Contenu d’apprentissage : C2.1
Processus mathématiques : Sélection d’outils et de stratégies, Représentation
Représente l’addition de ces monômes à l’aide d’au moins une représentation concrète et une représentation semi-concrète. \(3m + 2n + 4n + 5m\)
Contenu d’apprentissage : C2.1
Processus mathématiques : Sélection d’outils et de stratégies, Représentation
Représente les opérations de ces monômes à l’aide d’au moins une représentation concrète et une représentation semi-concrète. \(3m – 2n + 4n – 5m\)
Contenu d’apprentissage : C2.1
Processus mathématiques : Sélection d’outils et de stratégies, Représentation
Représente ces opérations à l’aide d’au moins une représentation concrète et une représentation semi-concrète.
- \(-3m + (-2)n + 4n – 5m\)
- \((-3a + 2b) + (4a + (-3)b)\)
Contenus d’apprentissage : C1.2, 1.3, 1.4
Processus mathématiques : Sélection d’outils et de stratégies
Simplifie cette expression algébrique en utilisant au moins deux stratégies.
\(-3x(4x – 3) – 5(4x^2 – 6x + 7)\)
Évaluer des expressions algébriques
Contenu d’apprentissage : C2.2
Processus mathématiques : Sélection d’outils et de stratégies
Sachant que le périmètre d’un rectangle peut être déterminé à l’aide de la formule \(P=2b+2h\), détermine le périmètre d’un rectangle dont la base mesure 12,5 cm et la hauteur mesure 45,2 cm.
Contenu d’apprentissage : C2.2
Processus mathématiques : Sélection d’outils et de stratégies
Le coût de location des diverses planches à roulettes du magasin Roulons ensemble peut être calculé à l’aide de la formule \(C=50+ph\), où \(p\) représente le coût par heure pour le type de planche louée et \(h\) la durée de la location en heures.
Quel sera le coût total pour louer une planche qui coûte 4,25 $ de l’heure pendant cinq heures?
Contenu d’apprentissage : C2.2
Processus mathématiques : Sélection d’outils et de stratégies
Évalue l’expression \(3\left(\frac{1}{3}a+b\right)\) si \(a=\frac{3}{4}\) et \(b=\frac{5}{3}\).
Contenu d’apprentissage : C1.5
Processus mathématiques : Sélection d’outils et de stratégies
Détermine si le point \(\left(\frac{7}{5},\frac{6}{5}\right)\) est sur la droite définie par l’équation \(y=-\frac{3}{5}x+2\).
Les équations algébriques
Contenu d’apprentissage : C2.3
Processus mathématiques : Raisonnement et justification
Comme solution à cette équation, Amid a obtenu 9, alors que Marcie a obtenu 3. Qui a raison et comment le sais-tu?
\(4a-12=15+9\)
Contenu d’apprentissage : C2.3
Processus mathématiques : Raisonnement et justification
Sans résoudre l’équation, comment peux-tu savoir que la solution doit être une valeur négative?
\(5x+12=3x+4\)
Contenu d’apprentissage : C2.3
Processus mathématiques : Raisonnement et justification
Quelle serait une bonne estimation de la valeur de \(x\) pour que l’équation \(29x−59=61x+28\) soit vraie? Explique ton raisonnement.
Contenu d’apprentissage : C4.2
Processus mathématiques : Représentation
Représente toutes les combinaisons possibles de deux nombres, \(x\) et \(y\), pour lesquelles \(2x+y=24\).
Les inéquations algébriques
Contenu d’apprentissage : C2.4
Processus mathématiques : Communication
Écris un scénario qui pourrait être représenté par l’inéquation \(2m+3 ≥ 15\).
Contenu d’apprentissage : C2.4
Processus mathématiques : Réflexion
Écris une inéquation composée d’au moins quatre termes dont la solution peut être représentée par la demi-droite orange suivante.

Contenu d’apprentissage : C2.4
Processus mathématiques : Réflexion
Laquelle des deux droites représente la solution de l’inéquation \(3x-5<2x-3\)? Comment le sais-tu?
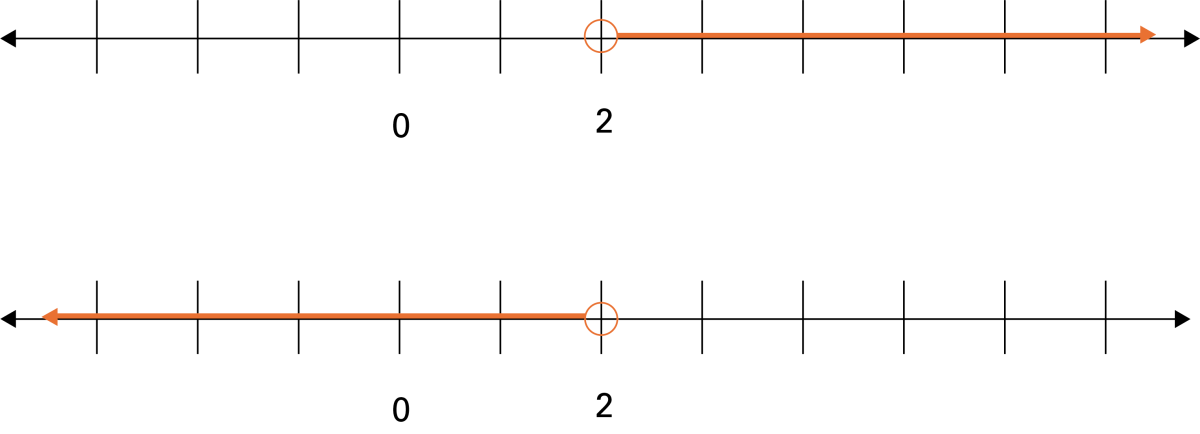
Les points zéro et deux sont identifiés. Le point deux est encerclé, et, une ligne fléchée orange par de ce point et se poursuit vers la droite. Une autre droite numérique graduée. Les points zéro et deux sont identifiés. Le point deux est encerclé, et, une ligne fléchée orange par de ce point et se poursuit vers la gauche.
Contenu d’apprentissage : C4.2
Processus mathématiques : Réflexion
Laquelle des deux inéquations aura le plus de solutions? Comment le sais-tu?
\(2x>36\) ou \(2x\ge 36\).
Réflexion
- En quoi les connaissances antérieures des élèves influencent-elles leur compréhension des concepts algébriques de 9e année et comment ces connaissances peuvent-elles être utilisées pour favoriser un apprentissage plus approfondi des concepts algébriques?
- En quoi les différentes pratiques pédagogiques influencent-elles le développement du raisonnement algébrique chez les élèves, et quelles stratégies spécifiques peuvent maximiser cet impact à long terme tout en s’adaptant aux besoins individuels des élèves?
