Géométrie et mesure : Mesure
Liens avec les autres domaines
Notre environnement est rempli d’objets composés de formes géométriques de base. En ayant l’occasion de résoudre des problèmes basés sur des situations issues de notre environnement, les élèves voient les mathématiques comme faisant partie intégrante de leur vie quotidienne. Ce type de problèmes aide les élèves à comprendre que tous les domaines des mathématiques sont interreliés et forment un tout.
Les exemples ci-dessous illustrent la manière dont la compréhension et l’application des autres domaines peuvent être intégrées dans le domaine Géométrie et mesure.
En examinant chaque question, réfléchissez aux attentes et aux contenus d’apprentissages du domaine Géométrie et mesure dont les élèves ont besoin pour y répondre ainsi qu’aux liens avec les concepts clés.
Nombres : Rapport
Contenus d’apprentissage : B3.5, E1.5
Processus mathématiques : Résolution de problèmes, Sélection d’outils et de stratégies, Établissement de liens
Tu dois construire une ferme de toit avec une pente ayant un rapport de 5 : 12 entre la hauteur et la demi-base pour une remise.
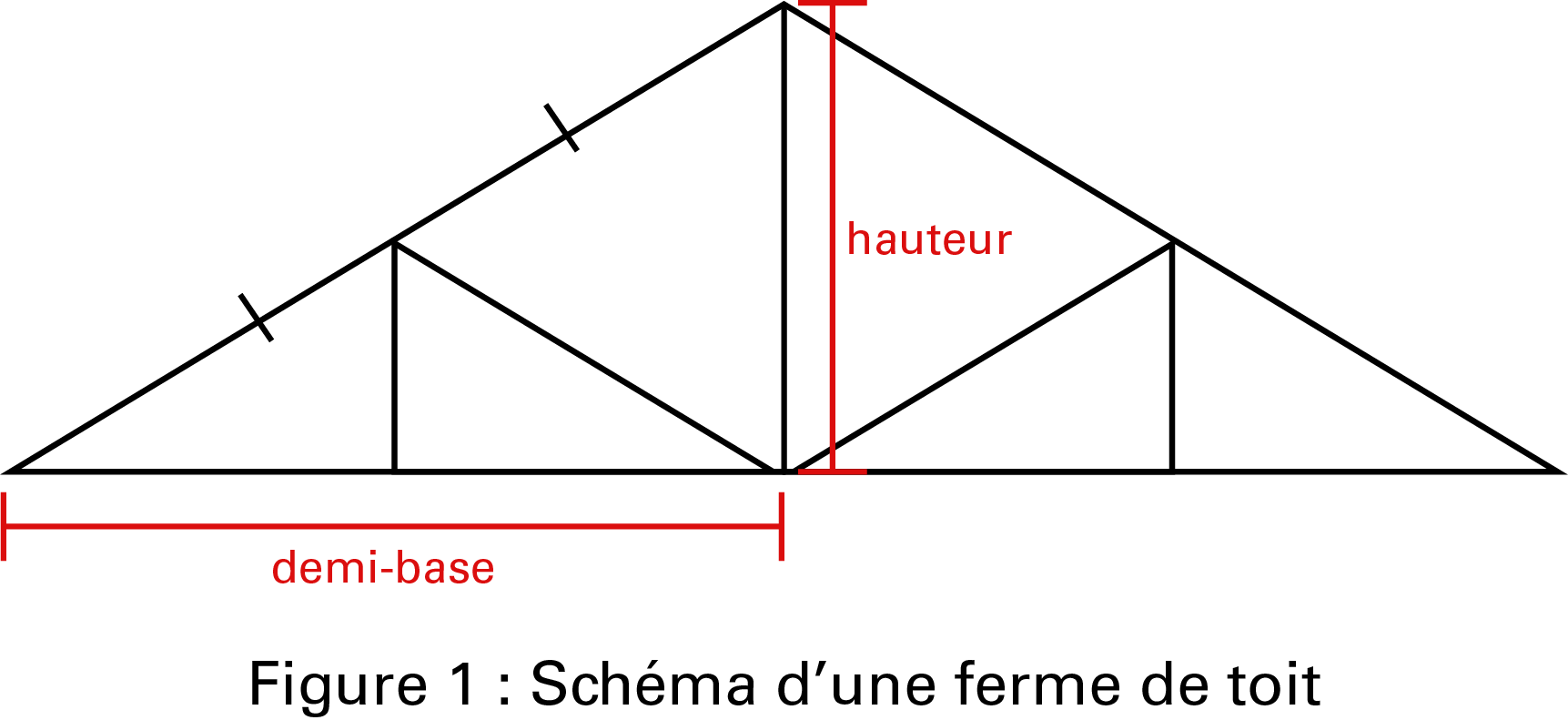
Grand triangle isocèle divisé en plusieurs petits triangles par 5 lignes. Une ligne verticale au milieu le divise en deux triangles rectangles identiques et représente la hauteur. Sous celui de gauche, il est écrit « demi-base ». Chaque demie est divisée de la même façon en trois triangles : il y a deux triangles rectangles identiques et un triangle équilatéral.
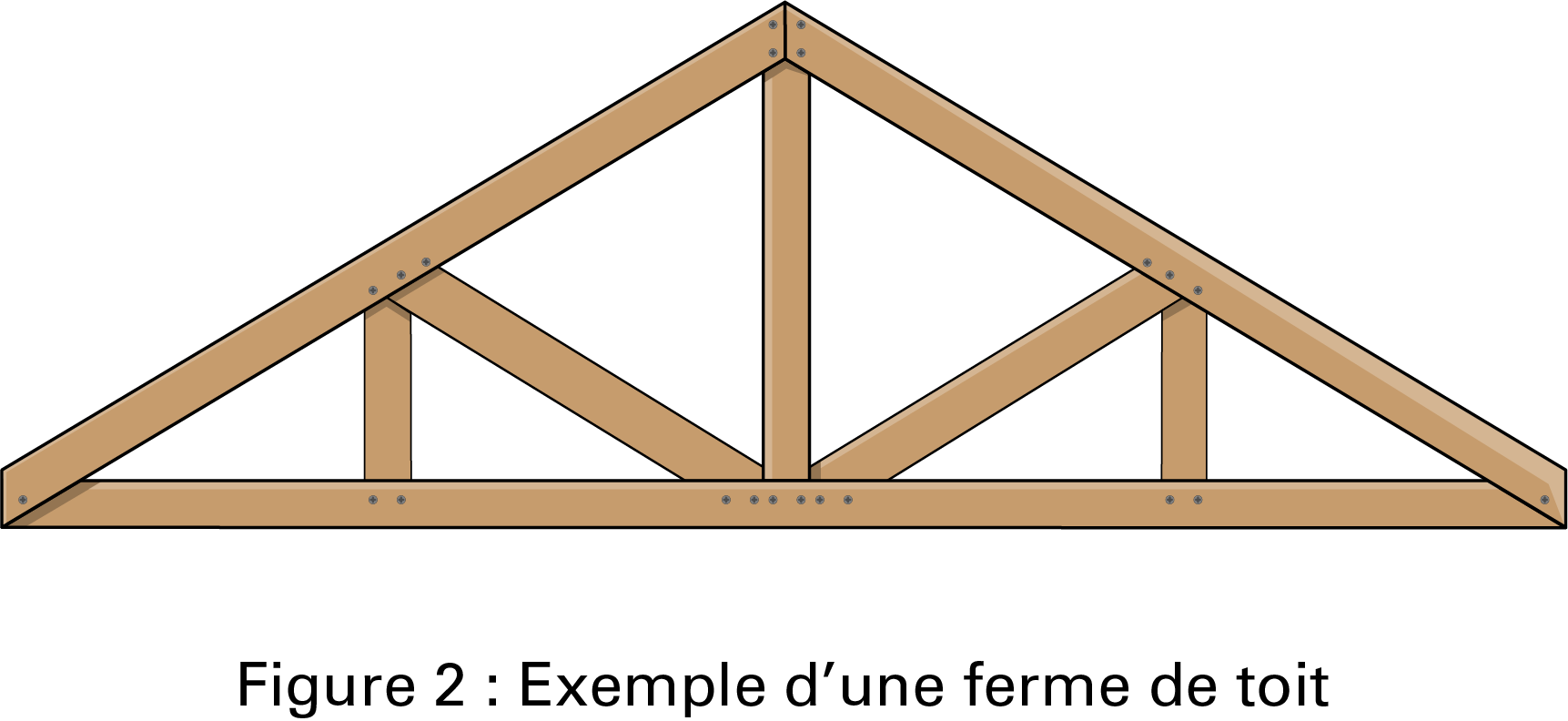
Chaque ferme de toit doit avoir 18 pieds de long à la base.
- Détermine la longueur totale de bois nécessaire pour construire une ferme de toit.
- Le bois pour construire la ferme de toit se vend en madrier d’une longueur de 8, 12 ou 20 pieds. Combien de madriers de chaque longueur devrais-tu acheter si tu dois installer des fermes de toit tous les 16 pouces sur un toit ayant 12 pieds de longueur? N’oublie pas de considérer les pertes, puisque chaque morceau de bois doit être coupé en angle.
Algèbre : Relations linéaire et non linéaire
Contenus d’apprentissage : C3.1, C4.1, E1.4
Processus mathématiques : Résolution de problèmes, Représentations
Imagine un cylindre dont le rayon est de 0,1 cm et la hauteur de 0,1 cm, donc ayant un volume de 0,001π cm3.
- Imagine que l’on double sa hauteur, puis en détermine le volume. On double à nouveau la hauteur, puis en détermine le volume. On répète ceci à plusieurs reprises.
Représente, à l’aide d’une table de valeur et d’un graphique, le volume du cylindre en fonction de sa hauteur si tu doubles celle-ci à chaque fois tout en conservant un rayon de 0,1 cm. - On refait le même exercice, mais en doublant le rayon au lieu de la hauteur.
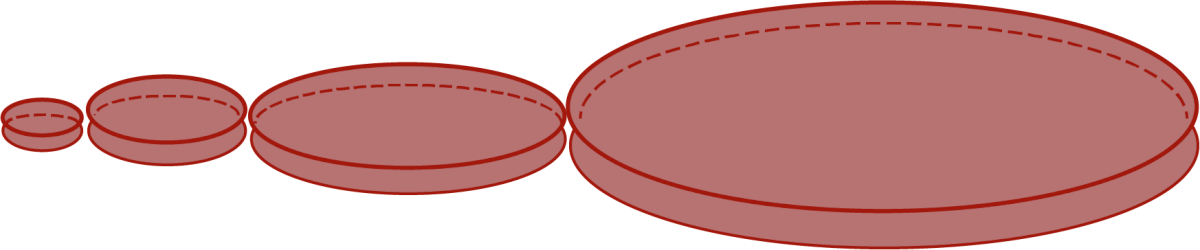Représente, à l’aide d’une table de valeur et d’un graphique, le volume du cylindre en fonction du rayon si tu doubles celui-ci à chaque fois tout en conservant une hauteur de 0,1 cm. - Quelles sont les différences et les ressemblances entre les deux situations?
- Que peux-tu affirmer au sujet du volume d’un cylindre lorsque tu doubles sa hauteur? Et lorsque tu doubles son rayon?
Données : Modèle mathématique
Contenus d’apprentissage : D1.3, D2.4, E1.5
Processus mathématiques : Résolution de problèmes, Réflexion
La réduflation est une stratégie commerciale qui consiste à réduire la quantité d’un produit pour le même prix. Par exemple, un contenant de jus d’orange de 2 L a diminué à 1,89 L. Il y a peu de différence pour l’œil humain.
- Choisis un produit qui se retrouve dans un emballage en carton (par exemple, des céréales, des craquelins, des pâtes).
- Trouve les dimensions du contenant ainsi que le poids du produit.
- En moyenne, les compagnies réduisent le poids d’environ 5 % sans que la consommatrice ou le consommateur y voient une différence. Crée un modèle mathématique montrant la relation entre la diminution de la quantité d’emballage nécessaire et la diminution du poids du produit pour la production de 100 000 emballages.
Littératie financière : Emprunt
Contenus d’apprentissage : E1.3, E1.6, F1.3
Processus mathématiques : Représentation, Résolution de problèmes
La ferme Au bon grain doit changer son silo à grains. Voici le genre de silos désiré. La partie cylindrique est construite en ajoutant des anneaux d’une hauteur de 2 pieds et 2 pouces chacun, un par-dessus l’autre.
Voici l’information du modèle de base du silo :
Diamètre : 18 pieds
Nombre d’anneaux de la partie cylindrique : 6
Chaque anneau a une hauteur de 2 pieds et 8 pouces.
Capacité maximale de la partie cylindrique (ou le grain est entreposé) : 85 m3
Coût : 26 000 $ (5 000 $ pour le toit, 3 500 $ par anneau)
Options possibles :
- Les propriétaires souhaitent entreposer environ 375 m3 de grain. Voici les autres dimensions possibles pour son silo comparativement au modèle de base.
- 1,5 fois le diamètre
- 1,5 fois le nombre d’anneaux
- 2 fois le diamètre
- 2 fois le nombre d’anneaux
Que leur recommanderais-tu d’acheter?
Coût : À partir du modèle de base, pour chaque augmentation de 3 pieds du diamètre, le coût du toit augmente de 500 $ et celui des anneaux de 525 $.
- Détermine le coût du silo que tu as recommandé. Ta recommandation devrait-elle changer? Explique ta réponse.
- L’institution financière a approuvé un prêt de 50 000 $ à un taux d’intérêt de 4,5 % par année pour l’aider dans cet achat. Les propriétaires ont un montant de 30 000 $ d’économisé qui peut être utilisé pour cet achat. Ils doivent prendre des décisions sur certains éléments du prêt :
- Quel sera le montant emprunté? Devraient-ils utiliser une partie ou la totalité de leurs économies pour diminuer le montant emprunté?
- Quelle devrait être la durée de leur prêt? 15, 20 ou 25 ans?
- Devraient-ils faire des versements mensuels ou aux deux semaines?
Tâche multidomaines
Contenus d’apprentissage : B3.5, D2.4, D2.5, E1.3, F1.4
Processus mathématiques : Sélection d’outils et de stratégies, Raisonnement et justification, Réflexion, Communication, Représentation
Dans le cadre de leur projet de classe, les élèves doivent concevoir et construire une maquette d’un monument célèbre du monde entier. Elles et ils ont choisi de reproduire la pyramide de Khéops en Égypte. Cependant, les élèves doivent résoudre un problème : les dimensions réelles de la pyramide de Khéops sont données en unités métriques, tandis que les matériaux utilisés pour construire la maquette sont mesurés en unités impériales.
- La hauteur de la pyramide de Khéops est de 138,8 mètres. La base de la pyramide de Khéops est un carré dont chaque côté mesure 230,4 mètres. Convertis ces mesures en unités compatibles pour déterminer la quantité de matériel nécessaire.
- Crée un plan à l’échelle de la maquette. La hauteur totale de la maquette ne doit pas dépasser 2 pieds. Les élèves peuvent utiliser des outils technologiques, tels qu’un logiciel de modélisation 3D, pour représenter la maquette de la pyramide de Khéops à l’échelle.
- Effectue une recherche pour déterminer les matériaux de construction disponibles (par exemple, du carton ondulé, du bois de balsa) et leur coût. En utilisant diverses représentations, tels des tableaux, des diagrammes, des tables de valeur ou des graphiques, compare les coûts des matériaux pour construire leur maquette.
- Présente un budget en justifiant les dimensions et les matériaux choisis.
Réflexion
- Comment peut-on intégrer et évaluer les attentes de divers domaines à travers l’analyse et la résolution de problèmes riches de mesure?
- Comment peut-on inciter les élèves à reconnaître et à réfléchir sur la manière dont leur compréhension des nombres et de l’algèbre se manifeste dans divers contextes associés à l’étude de la mesure?
- Qu’est-ce qui pourrait être modifié dans mes stratégies pédagogiques pour encourager les élèves à persévérer dans l’approfondissement de leur compréhension conceptuelle des mathématiques à travers la résolution de problèmes riches et authentiques?