Géométrie et mesure : Mesure
Liens entre les années d’études
Figures planes
Contenu d’apprentissage : E2.4
Processus mathématiques : Résolution de problèmes, Sélection d’outils et de stratégies
Lucas souhaite aménager une partie de son jardin pour y planter des fleurs et des légumes.
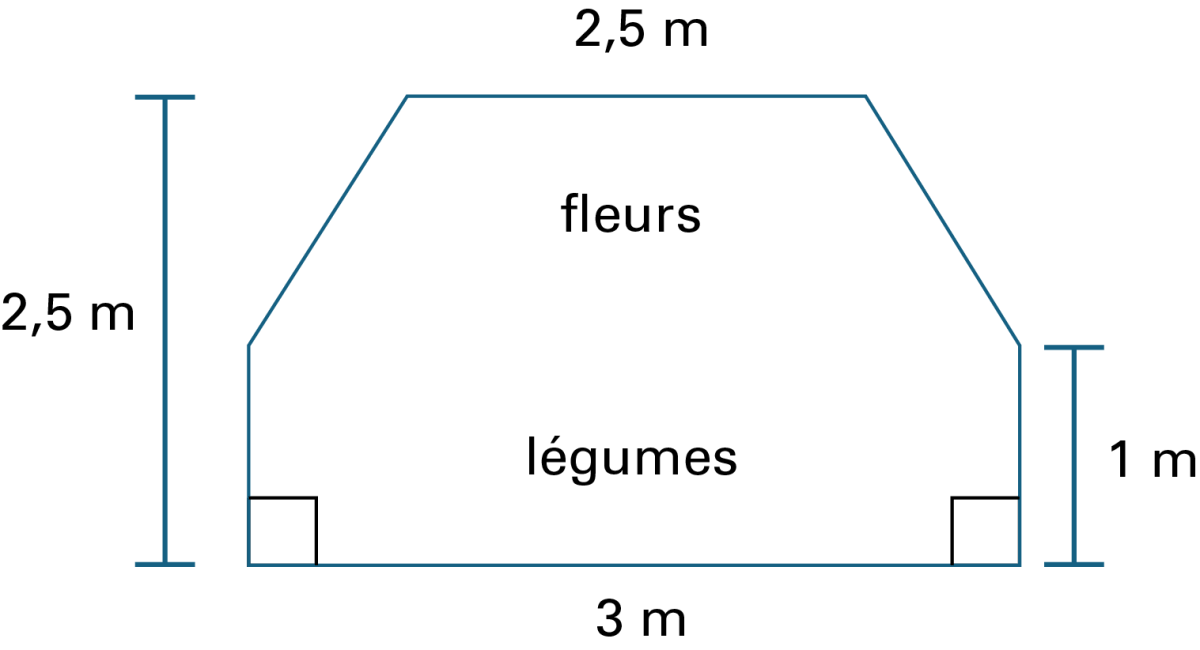
La hauteur de l’hexagone est de 2 mètres cinquante. La mesure de la base est 3 mètres. Les côtés perpendiculaires à la base sont d’un mètre. Le côté parallèle à la base est de 2 mètres cinquante. Le mot « légumes » est écrit au-dessus de la base et un peu plus haut le mot « fleur »
Calcule l’aire totale du jardin afin de déterminer la grandeur de toile dont il aura besoin pour le recouvrir durant l’hiver.
Contenus d’apprentissage : E2.2, E2.3, E2.7
Processus mathématiques : Résolution de problèmes, Sélection d’outils et de stratégies
Marie souhaite aménager un potager dans son jardin en utilisant une partie rectangulaire pour les légumes et une partie circulaire pour les herbes aromatiques.

Le demi-cercle est à la droite du rectangle. Dans le rectangle, il y a le mot « légumes » et le mot « herbes aromatiques » est dans le demi-cercle. La longueur totale de la forme est de 3 mètres cinquante. Sa hauteur est de 2 mètres soixante.
- Quelle quantité de grillage est requise pour clôturer le jardin?
- Combien de mètres cubes de terre Marie a-t-elle besoin pour son potager si elle doit ajouter 10 cm d’épaisseur de terre?
- Quelle quantité de paillis est nécessaire pour recouvrir le sol de la partie circulaire des herbes aromatiques?
Contenus d’apprentissage : E2.3, E2.4
Processus mathématiques : Résolution de problèmes, Sélection d’outils et de stratégies
Kim souhaite aménager un potager qu’il faudra clôturer afin d’empêcher les animaux d’aller y manger les légumes.
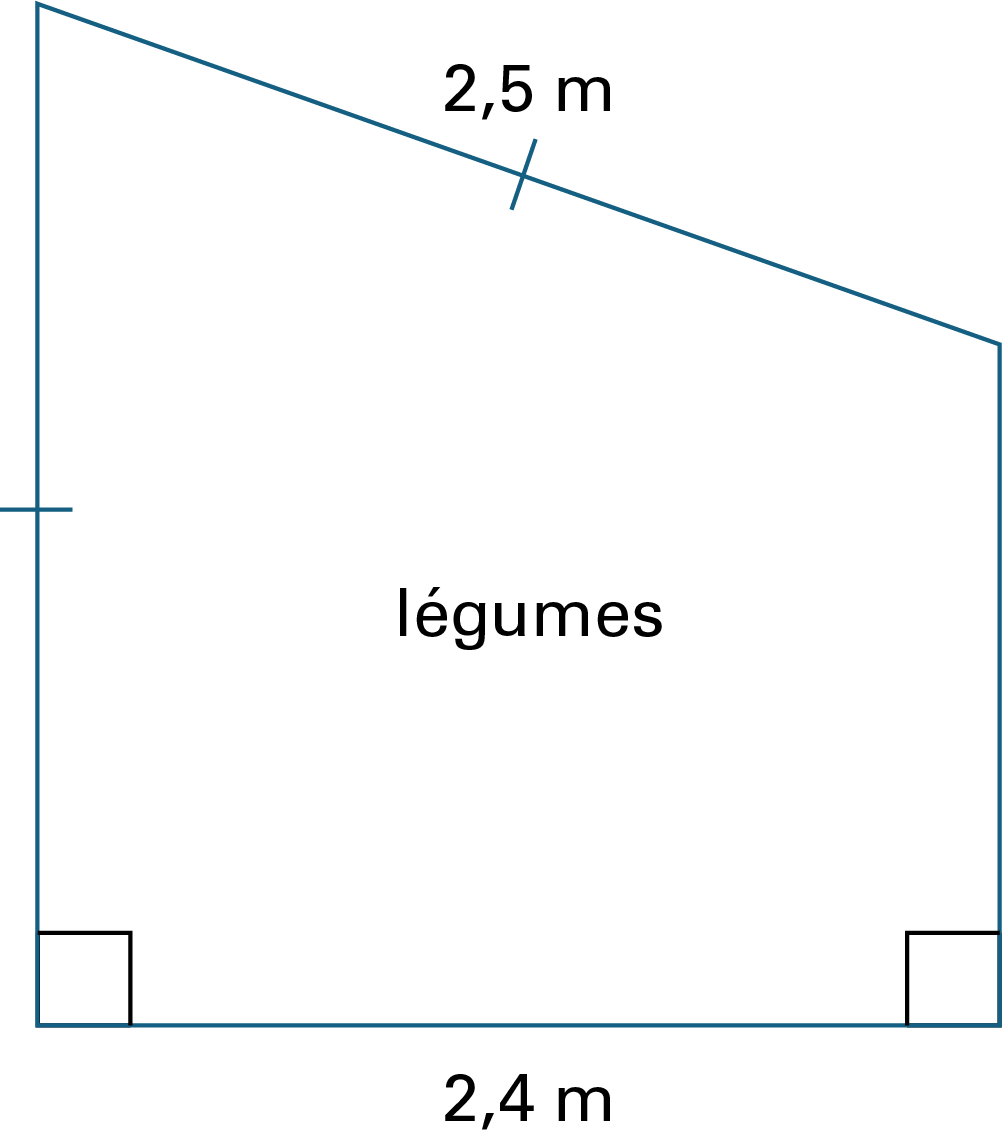
La base possède deux angles droits et mesure 2,4 mètres. Le côté oblique, en haut, mesure 2,5 mètres.
Combien de mètres de clôture Kim a-t-elle besoin?
Contenu d’apprentissage : E1.4
Processus mathématiques : Résolution de problèmes, Raisonnement et justification, Réflexion, Représentation, Sélection d’outils et de stratégies
Dans un jardin rectangulaire de 10 mètres de longueur et de 8 mètres de largeur, le propriétaire souhaite agrandir la surface de plantation en augmentant la longueur et la largeur du même nombre de mètres.
- En utilisant un logiciel de modélisation 3D, détermine l’effet sur la surface du jardin si le propriétaire décide d’augmenter la longueur et la largeur de 3 mètres.
- Avec le même outil, détermine la façon dont cette augmentation de la longueur et de la largeur affecte le périmètre du jardin.
- Utilise tes résultats pour montrer la façon dont la modification simultanée des dimensions d’une figure plane, comme un jardin rectangulaire, affecte à la fois sa surface et son périmètre.
- Propose une méthode mathématique générale pour calculer la variation de la surface et du périmètre d’un rectangle lorsque ses dimensions sont modifiées proportionnellement.
Solides
Contenu d’apprentissage : E2.1
Processus mathématiques : Résolution de problèmes, Sélection d’outils et de stratégies
Dans la vie quotidienne, il est souvent nécessaire de mesurer plusieurs objets ou quantités pour en déterminer le volume ou la capacité.
- Décris une situation de la vie quotidienne où il serait plus approprié d’utiliser une petite unité de mesure, une unité de mesure moyenne ou une grande unité de mesure pour en déterminer la capacité. Spécifie l’unité de mesure utilisée.
- Explique la raison pour laquelle cette unité de mesure serait plus appropriée dans chaque situation.
Contenu d’apprentissage : E2.7
Processus mathématiques : Résolution de problèmes, Sélection d’outils et de stratégies
Sarah souhaite construire un petit étang circulaire dans son jardin pour y élever des poissons. Elle prévoit utiliser un grand cylindre en plastique qui a un diamètre de 2,4 mètres et une profondeur de 1,6 mètre comme réservoir.
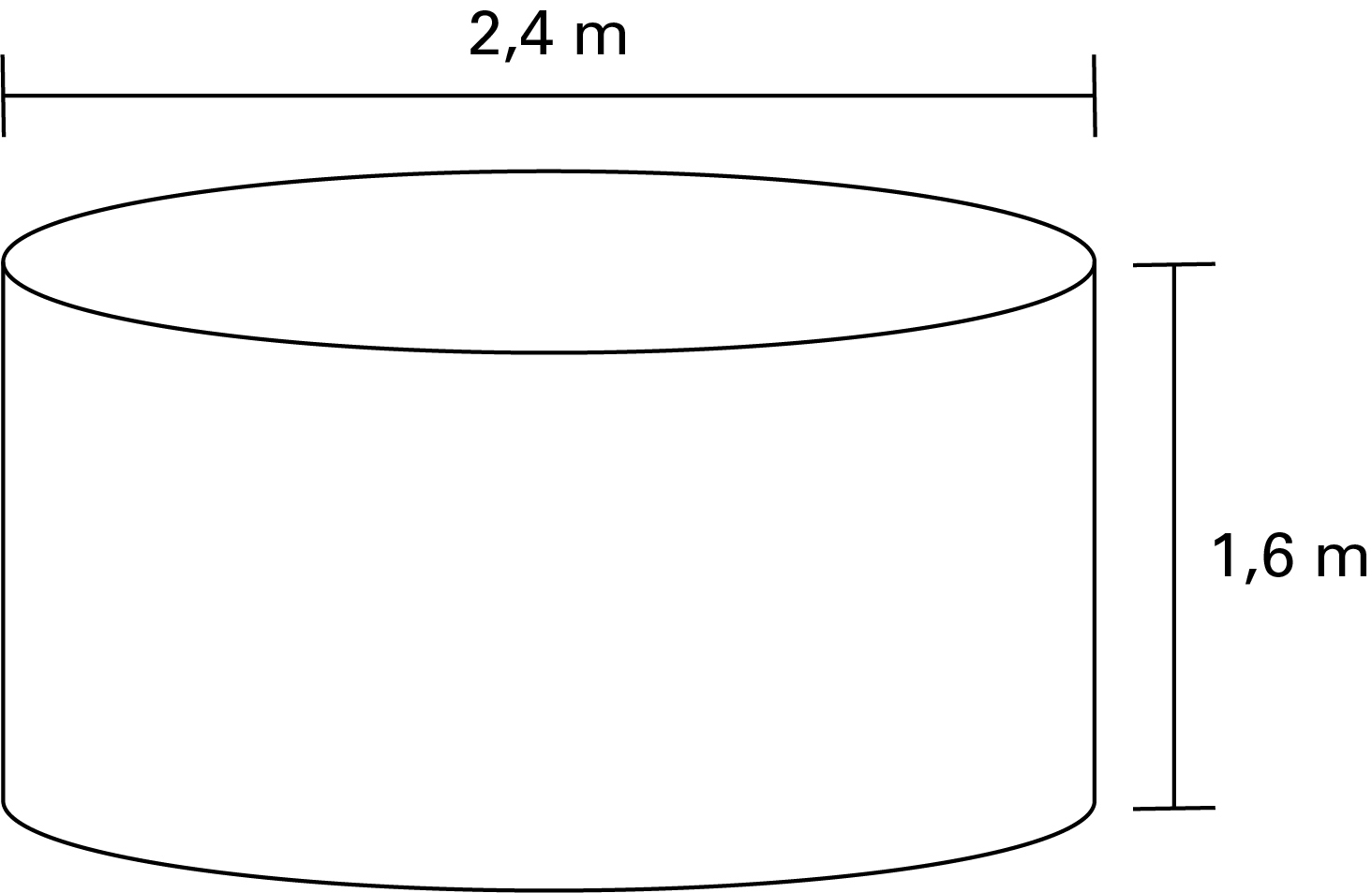
Si Sarah souhaite remplir le cylindre à 80 % de sa capacité, combien de litres d’eau aura-t-elle besoin?
Contenu d’apprentissage : E2.3
Processus mathématiques : Résolution de problèmes, Réflexion
Conçois une boîte à lunch composée d’un prisme et d’un demi-cylindre qui aura une capacité entre 1,5 et 2 L (1 L = 1 000 cm3).
Contenu d’apprentissage : E1.4
Processus mathématiques : Résolution de problèmes, Réflexion
Noah possède une boîte en bois en forme de prisme rectangulaire pour ses objets précieux. Il souhaite fabriquer une nouvelle boîte ayant un volume deux fois plus grand que l’originale. Comment devrait-il ajuster les dimensions de la nouvelle boîte par rapport à celles de sa boîte actuelle?
Réflexion
- En quoi la diversité des objets à deux et à trois dimensions présents dans notre environnement peut-elle être exploitée pour engager les élèves dans des tâches authentiques et enrichissantes?
- Quelles opportunités de collaboration avec une ou un collègue peuvent être explorées pour réaliser un projet interdisciplinaire?
