Nombres : Nombres réels
Concepts clés
Les nombres réels
- Le système des nombres réels est composé de nombres rationnels et irrationnels.
- Chaque nombre réel possède deux attributs : la grandeur et le signe.
Les nombres rationnels
- Les nombres naturels, les nombres entiers, certains nombres décimaux ainsi que les fractions et les nombres fractionnaires sont des sous-ensembles des nombres rationnels.
- Nombre qui peut être exprimé sous la forme \(\frac{a}{b}\), où a et b sont des entiers, et b ≠ 0 (par exemple : 4, 0, \(\frac{2}{3}\), \(\frac{-9}{5}\)).
- Nombre qui peut être exprimé sous la forme décimale qui comporte une suite finie de chiffres à la droite de la virgule décimale ou une suite infinie et périodique de chiffres (par exemple : \(1,\overline{625}; 0,5; 4,75\)).
Les nombres irrationnels
Nombre qui ne peut être exprimé comme quotient d’entiers. Sous la forme décimale, ce nombre est toujours une suite infinie et non périodique de chiffres à la droite de la virgule décimale (par exemple : \(3,13159…; \sqrt{2}; 4,515 515 551…; \pi \)).
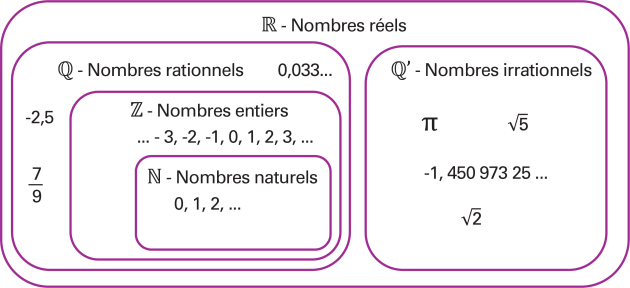
Dans ce dernier il y a 2 sous-ensembles : les nombres rationnels représentés par le symbole « Q » et les nombres irrationnels représentés par le symbole « Q » prime. Des exemples de nombres rationnels sont : « 33 millièmes ; négatif 2 et 5 dixième ; 7 sur 9 ». Dans le sous-ensemble des nombres rationnels, il y a un plus petit ensemble qui s’appelle nombres entiers représentés par le symbole « Z ». Des exemples de nombres entiers sont « moins 3 ; moins 2 ; moins 1 ; zéro ; un ; 2 ; 3, et cetera ». Puis dans cet ensemble il y en a un autre ensemble qui s’appelle les nombres naturels, représentés par le symbole « N ». Des exemples de nombres naturels sont : « zéro ; un ; 2 ; 3, et cetera ». Il n’y a pas de sous-ensemble pour les nombres irrationnels. Des exemples de nombres irrationnels sont « Pi ; racine carrée de 5 ; négatif un virgule 4 5 0 9 7 3 2 5 continuant; racine carrée de 2 ».
Densité, infini et limite
- La densité peut être vue comme la probabilité de choisir un nombre dans un sous-ensemble donné. Ce concept peut être utilisé pour comparer la densité de deux sous-ensembles. Par exemple, l’ensemble des nombres carrés entre 0 et 100 est moins dense que l’ensemble des nombres impairs entre 0 et 100, puisqu’il y a plus de nombres dans le 2e ensemble.
- L’infini est un concept qui sert à caractériser des ensembles et certains nombres décimaux. Par exemple, l’ensemble des nombres entiers est infini, les nombres décimaux irrationnels ont une infinité de chiffres après la virgule décimale.
- La limite d’une suite ou d’une fonction peut être déterminée en observant son comportement à long terme. Par exemple, si on observe la suite 9, 3, 1, \(\frac{1}{3}\), \(\frac{1}{9}\), …, on peut en déduire que la limite sera 0.
Représentations numériques
Les nombres peuvent être représentés numériquement de différentes manières.
En voici quelques exemples :
| Forme standard | Forme développée | Notation exponentielle | Notation scientifique |
|---|---|---|---|
| \(16\frac{1}{9}\) | \( 16 + \frac{1}{9}\) | \(2^4 + \frac{1}{3^2}\) ou \(2^4+3^{-2}\) | |
| \(-192\) |
\(\left(-100\right)+\left(-90\right)+\left(-2\right)\) \(-1\times 2\times 2\times 2\times 2\times 2\times 2\times 3\ \) |
\(\left(-1\times 10^2\right)+\left(-9\times 10^1\right)+\left(-2\times 10^0\right)\) \( –2^6\times 3\) |
\(-1,92\times 10^2\) |
| \(51,25\) | \(50+1+0,2+0,05\ \) | \(\left(5\times 10^1\right)+\left(1\times 10^0\right)+\left(2\times 10^{-1}\right)+\left(5\times 10^{-2}\right)\) | \(5,125\times 10^1\) |
Les nombres entiers et les fractions décimales positives et négatives peuvent être exprimés sous la forme décimale dont le développement est fini.
Opérations
- Les actions dans une situation influencent le choix de l’opération. La même opération peut décrire des situations différentes :
- Des situations qui impliquent des changements (ajout ou retrait), des réunions ou des comparaisons peuvent être représentées par l’addition ou la soustraction.
- Des situations qui impliquent des groupes égaux (groupement d’additions ou de soustractions répétées, partage), des taux, des comparaisons de rapports ou des dispositions rectangulaires peuvent être représentées au moyen d’une multiplication ou d’une division.
- Les nombres peuvent être décomposés en parties. Un nombre peut être composé en combinant des parties. La décomposition et la composition de nombres peuvent être utilisées comme stratégie pour opérer sur des nombres. Par exemple : \(-3\frac{1}{4}+5\frac{3}{8}\) peut être décomposé en \(-3+\left(-\frac{1}{8}\right)+\left(-\frac{1}{8}\right)+5+\frac{1}{8}+\frac{1}{8}+\frac{1}{8}\) afin d’utiliser la commutativité et les opposés pour simplifier les opérations \(-3+5+\left[\left(-\frac{1}{8}\right)+\left(\frac{1}{8}\right)\right]+\left[\left(-\frac{1}{8}\right)+\left(\frac{1}{8}\right)\right]+\frac{1}{8}\) et obtenir \(2\frac{1}{8}\).
- Factoriser un nombre, c’est l’exprimer sous la forme d’un produit de nombres ou facteurs plus petits. Par exemple, 10 peut être factorisé par \(5 \ \times 2\) où 5 et 2 sont des facteurs de 10.
- Les éléments neutres et absorbants ainsi que les propriétés des opérations telles que la commutativité, l’associativité et la distributivité peuvent être appliqués à tout type de nombre.
- Élément absorbant : \(a \times 0 = 0, \, 0\,(x\, – a) = 0\).
- Élément neutre : \(a + 0 = a, \, a - 0 = a, \, a \times 1 = a, \, a \div 1 = a\).
- Associativité : \((a + b) + c = a + (b + c), \, (a \times b) \times c = a \times (b \times c)\).
- Commutativité : \(a + b = b + a, \, a \times b = b \times a\).
- Distributivité : \(a \times (b + c) = (a \times b) + (a \times c)\).
- L’ordre des priorités des opérations doit être respecté lorsqu’une expression numérique comporte plusieurs opérations. Il s’agit d’une convention ou d’une règle utilisée pour simplifier des expressions numériques.
- Un nombre rationnel peut être utilisé pour estimer un nombre irrationnel.
Les nombres réels
Le tableau suivant résume les types de nombres avec lesquels les élèves travaillent pour chaque année d’études.
| Année d’études | Nombres naturels | Nombres entiers | Fractions | Nombres décimaux | Pourcentages | Nombres irrationnels |
|---|---|---|---|---|---|---|
| 1re | jusqu’à 50 |
|
||||
| 2e | jusqu’à 200 |
|
||||
| 3e | jusqu’à 1000 |
|
||||
| 4e | jusqu’à 10 000 | des demis aux dixièmes | dixièmes | |||
| 5e | jusqu’à 100 000 | des demis aux douzièmes | centièmes | Pourcentage de nombres naturels | ||
| 6e | jusqu’à un million | tous | toutes fractions positives | millièmes | Calculer mentalement 1 %, 5 %, 10 %, 15 %, 25 %, 50 % de nombres naturels. | |
| 7e | jusqu’à un milliard | tous |
|
nombres décimaux positifs | Calculer mentalement une augmentation ou une diminution de 1 %, 5 %, 10 %, 25 %, 50 %, 100 % de nombres naturels. | \(π\) |
| 8e | tous | tous |
|
nombres décimaux positifs | Tous les pourcentages, incluant ceux plus petits que 1 % et plus grands que 100 % | \(π, 2–\sqrt{2}, 4,15…\) |
| 9e | tous | tous | toutes | tous | tous | tous |
Réflexion
- En quoi la progression de l’apprentissage des fractions de la 1re à la 5e année soutient-elle l’apprentissage des fractions de la 6e à la 9e année?
- De quelle manière la compréhension des nombres entiers aide-t-elle à comprendre les fractions négatives et les nombres décimaux négatifs?
- Comment cette progression des différents types de nombres introduits aide-t-elle les élèves à développer une compréhension approfondie du système des nombres réels?
