Nombres : Nombres réels
Liens avec les autres domaines
Les nombres font partie intégrante de tous les domaines de mathématiques. En 9e année, les élèves font appel à leur compréhension du sens du nombre et des opérations afin de résoudre des problèmes dans une variété de contextes et de situations. Les exemples ci-dessous illustrent la manière dont le domaine Nombres est appliqué dans les autres domaines à l’étude.
En examinant chaque question, réfléchissez aux attentes et aux contenus d’apprentissages du domaine Nombres dont les élèves ont besoin pour y répondre ainsi qu’aux liens avec les concepts clés.
Algèbre : Résoudre des équations
Contenus d’apprentissage : B3.2, B3.5, C1.5
Processus mathématiques : Établissement de liens, Sélection d’outils et de stratégies
Une ou un élève détermine qu’elle ou il peut courir \(1\frac{1}{4}\) de tour de la piste en 2 minutes.
- Créer une équation : Détermine une équation pour montrer la relation entre le temps où elle ou il court, t, en minutes, et la distance qu’elle ou il parcourt, d, en nombre de tours.
- Faire des prédictions : Un tour de piste est d’une longueur de 400 mètres. En utilisant ton équation, détermine la quantité de minutes qu’il faut à l’élève pour courir 5 kilomètres.
Données : Mesures statistiques
Contenus d’apprentissage : B3.5, D1.2, D2.3
Processus mathématiques : Représentation, Sélection d’outils et de stratégies
Les élèves collectent et analysent des données sur les ventes de deux différents aliments à la cafétéria de l’école pendant une période de temps significative. Elles et ils utilisent leurs résultats pour calculer des pourcentages et des rapports, et représentent les données en utilisant des méthodes statistiques appropriées.
- Collecter des données : Pendant un temps approprié, enregistre le nombre de chaque type d’aliment choisi vendu chaque jour à la cafétéria de l’école.
- Calculer des pourcentages et des rapports : Détermine le pourcentage de chaque aliment choisi vendu par rapport aux ventes totales.
- Créer des représentations visuelles :
- Crée un diagramme circulaire pour montrer la distribution en pourcentage des ventes de chaque aliment choisi par rapport aux ventes totales.
- Fais une analyse statistique pour chaque type d’aliment choisi en utilisant des mesures de tendances centrales et des diagrammes de quartiles.
Géométrie et mesure : Nouvelles dimensions
Contenus d’apprentissage : B3.5, E1.3, E1.4
Processus mathématiques : Raisonnement et justification, Sélection d’outils et de stratégies
Les élèves reçoivent cette image ou un modèle fait avec du matériel (par exemple des cubes emboitables).
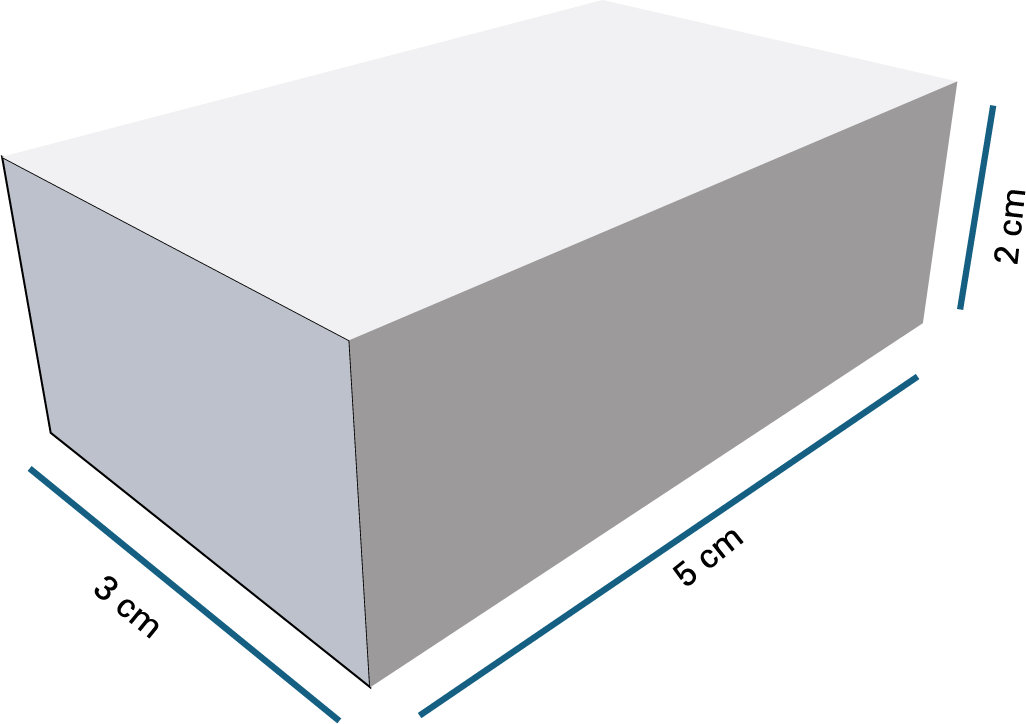
- Concevoir une boîte : Conçois une boîte similaire qui aura un volume 12 fois plus grand.
- Calculer l’aire totale : Détermine l’aire totale de la boîte.
- Déterminer la quantité de bois à acheter : Détermine la quantité de pieds carrés de bois nécessaire pour construire la boîte.
Littératie financière : Intérêts
Contenus d’apprentissage : B2.1, B3.5, F1.2, F1.3
Processus mathématiques : Réflexion, Sélection d’outils et de stratégies
Les élèves comparent différents plans d’épargne afin de déterminer celui qui offre le meilleur rendement sur une période donnée. Elles et ils calculent les intérêts, analysent les effets de différents taux d’intérêt et fréquences de composition, et étudient l’impact de dépôts supplémentaires.
- Rechercher des plans d’épargne : Indique trois plans d’épargne différents offerts par des institutions financières, ainsi que les détails sur les taux d’intérêt, la fréquence de capitalisation des intérêts et les frais supplémentaires.
- Calculer les intérêts : Pour chaque plan d’épargne, détermine le montant total qui serait accumulé sur une période de cinq ans, en commençant par un dépôt initial et en effectuant des dépôts mensuels réguliers, à l’aide d’outils financiers.
- Comparer les plans : Crée un tableau de comparaison montrant le montant total accumulé, les intérêts totaux gagnés et les frais pour chaque plan.
- Faire une recommandation : En te basant sur tes calculs, détermine le plan d’épargne qui offre le meilleur rendement et explique la raison de cette recommandation.
Tâche multidomaines
Contenus d’apprentissage : B3.5, C3.1, D1.2, D1.3
Processus mathématiques : Résolution de problèmes, Communication, Sélection d’outils et de stratégies
Les élèves effectueront une analyse des statistiques de performance de deux joueuses ou joueurs de basket-ball occupant la même position au cours d’une saison. (Il est possible de laisser les élèves choisir deux joueuses ou joueurs du sport de leur choix.) Elles et ils utiliseront des concepts issus des domaines Nombres, Algèbre et Données pour calculer des moyennes, créer des graphiques et modéliser des relations. L’utilisation de la technologie sert à mettre l’accent sur l’analyse des données et le fait de tirer des conclusions plutôt que la création des diagrammes.
- Collecter des données : À partir d’un tableau des statistiques de performance de joueuses ou de joueurs de basket-ball (par exemple, les points marqués par match, les passes décisives, le nombre de minutes jouées par match), sélectionne de trois à cinq données, puis organise-les de manière appropriée afin de faciliter une comparaison des deux athlètes.
- Calculer les mesures de tendance centrale : Détermine les mesures de tendances centrales pour chaque statistique choisie.
- Créer des représentations visuelles : Utilise des diagrammes de quartiles pour une ou deux statistiques pour chaque joueuse ou joueur afin de pouvoir comparer visuellement les performances des athlètes au cours de la saison.
- Modéliser des relations : Utilise les données pour créer un modèle linéaire ou non linéaire qui prédit les performances futures en fonction des tendances passées.
- Tirer des conclusions : À la suite de l’analyse des données, quelles suggestions pourrais-tu faire à la personne responsable de l’entraînement des deux athlètes?
Réflexion
- Qu’est-ce qui pourrait être repensé dans la planification pour donner l’occasion aux élèves de démontrer de manière plus riche et diversifiée leur compréhension approfondie du sens des nombres et des opérations mathématiques?
- Qu’est-ce qui pourrait être modifié et amélioré dans mes gestes pédagogiques pour encourager les élèves à explorer et à comprendre en profondeur l’application des nombres dans une variété de contextes mathématiques et de situations de la vie quotidienne?
