Nombres : Nombres réels

La sélection d’outils et de stratégies pédagogiques par le personnel enseignant doit être faite de manière réfléchie et ciblée, selon le contexte, l’intention et les besoins d’apprentissage. Ainsi, le personnel enseignant agit comme modèle et influence positivement le développement de la capacité des élèves de sélectionner des outils, des technologies et des stratégies lorsqu’elle et ils effectuent, illustrent et expliquent des idées et leur pensée mathématique.

Toutes et tous les élèves devraient être encouragés à choisir et à utiliser des outils pour illustrer les idées mathématiques. Les élèves finissent par comprendre que la création de leurs propres représentations est un moyen puissant de renforcer leur compréhension et d’expliquer leur raisonnement aux autres.

Lors de la représentation des nombres et de leurs opérations, différents outils et modèles peuvent être utilisés selon le contexte.

Type de modèle	Outils	Exemples
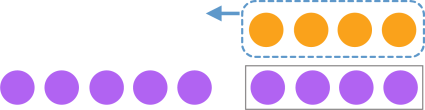
Ensemble	Matériel de base dix Tuiles carrées Jetons bicolores Cubes emboîtables Mosaïques géométriques	\((+5) – (–4) = (+9)\) Commencez à \((+5)\); puis afin d’enlever \((-4)\), le représenter à l’aide du principe de la paire nulle, ce qui donne un autre \((+4)\), pour arriver à \((+9)\).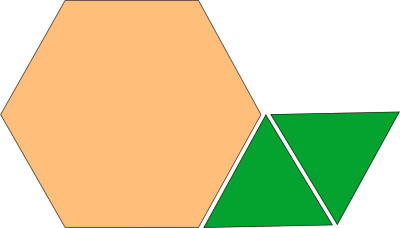 \(\frac{2}{3}\) des objets sont verts.
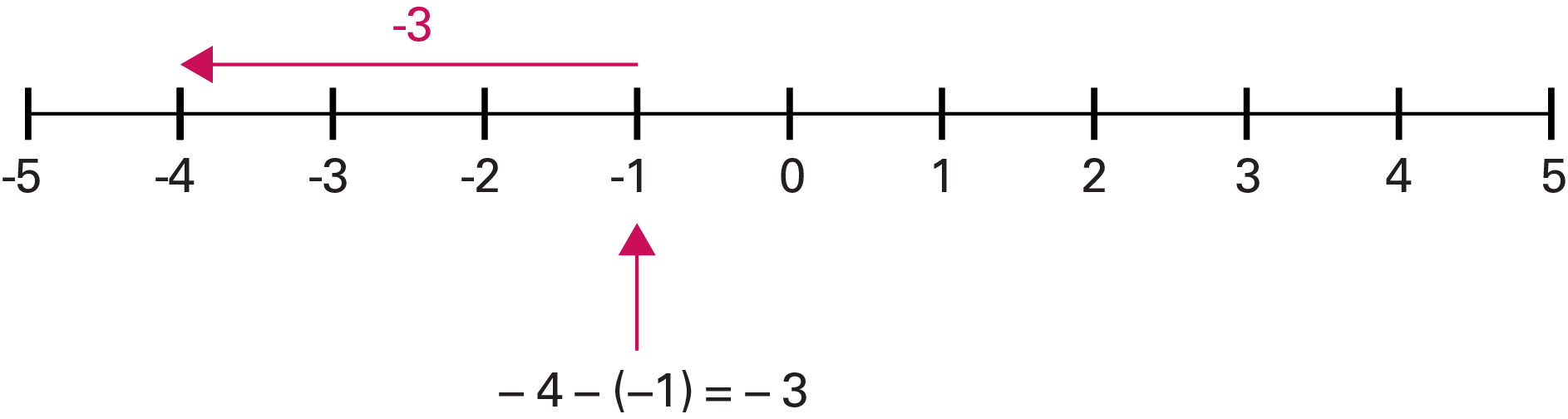
Linéaire	Droite numérique Droite numérique double Ruban à mesurer Bandes linéaires (par exemple, bandes de fractions) ou réglettes Géoplans	Au-dessus, une flèche rouge pointe de moins 1 à moins 4. Il est écrit : moins 3. En dessous, une flèche rouge pointe sur moins 1. Il est écrit : moins 4 moins parenthèse ouvrante moins 1 parenthèse fermante égale moins 3. Quelle distance dois-je parcourir, en partant de \((-1)\), pour me rendre à \((-4)\)?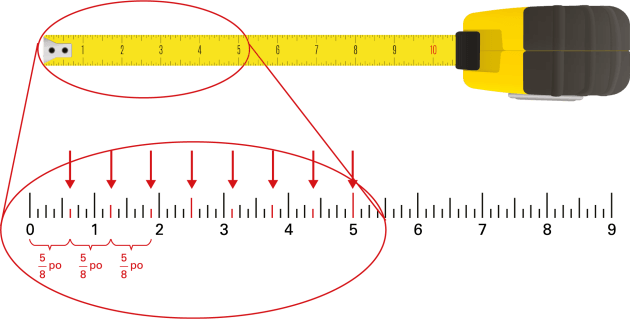 Les 5 premiers pouces sont encerclés en rouge. En dessous du ruban il y a un agrandissement des mesures. Les pouces sont représentés de zéro à 5. Entre chaque pouce est divisé en 8. Il y a des lignes qui permettent de mesurer les quarts, les tiers, et cetera. Une flèche rouge est placée à chaque 5 huitième, jusqu’au 5 pouces. Combien y a-t-il de \(\frac{5}{8}\) de pouces dans 3 pieds?
Surface	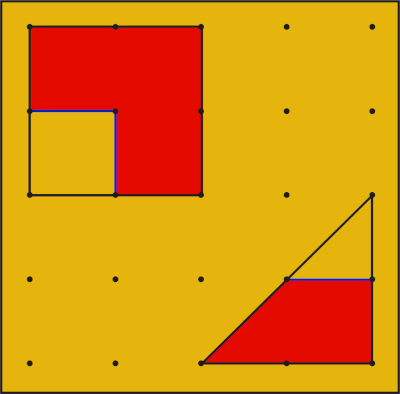Géoplans Grilles ​​Tuiles carrées Mosaïques géométriques Réglettes	Les 2 surfaces rouges représentent \(\frac{3}{4}\) de chaque figure. Un exposant 2, un cube. 2 exposant 2, 2 bâtonnets dont la longueur de chacun équivaut à 2 cubes. 3 exposant 2, 3 bâtonnets dont la longueur de chacun équivaut à 3 cubes. 4 exposant 2, 4 bâtonnets dont la longueur de chacun équivaut à 4 cubes. 5 exposant 2, 5 bâtonnets dont la longueur de chacun équivaut à 5 cubes. 6 exposant 2, 6 bâtonnets dont la longueur de chacun équivaut à 6 cubes. 7 exposant 2, 7 bâtonnets dont la longueur de chacun équivaut à 7 cubes. 8 exposant 2, 8 bâtonnets dont la longueur de chacun équivaut à 8 cubes. 9 exposant 2, 9 bâtonnets dont la longueur de chacun équivaut à 9 cubes. Dix exposant 2, dix bâtonnets dont la longueur de chacun équivaut à dix cubes. Régularité pour développer la compréhension des lois des exposants.
Volume Capacité	Cubes emboîtables Tasse à mesurer	La première est construite avec 24 cubes, la deuxième avec 12 cubes et la troisième avec 6 cubes. Comparer des volumes lorsque l’on modifie des dimensions.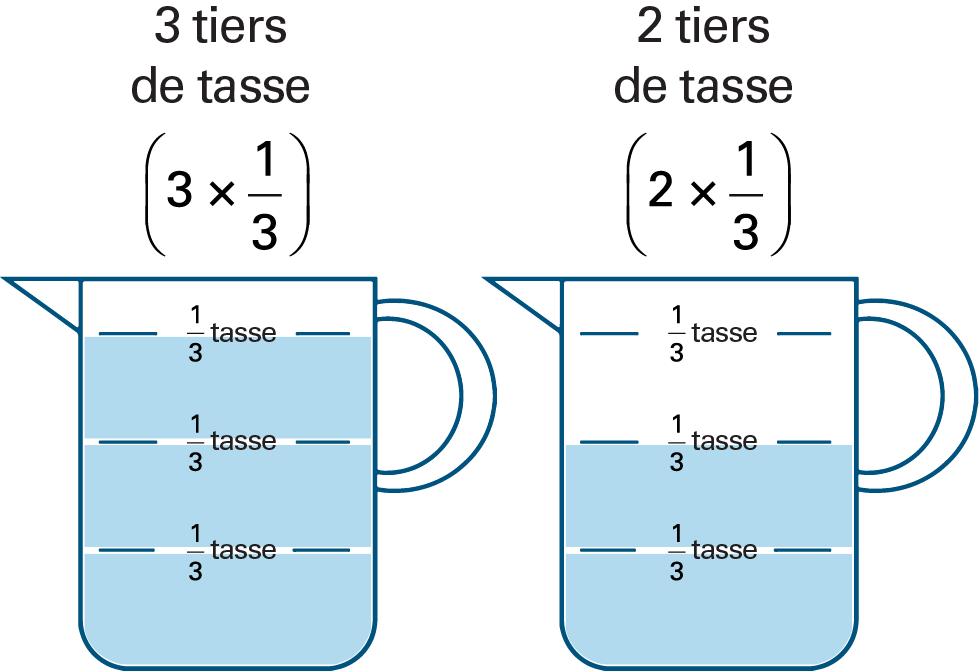 La première tasse est remplie aux trois tiers. Au-dessus, il est écrit : « 3 tiers de tasse. Parenthèse ouvrante, 3 fois un tiers, parenthèse fermante ». La deuxième tasse est remplie aux deux tiers. Au-dessus, il est écrit : « 2 tiers de tasse. Parenthèse ouvrante, 2 fois un tiers, parenthèse fermante ». Représentation de \(1\frac{2}{3}\) avec des fractions unitaires dans un contexte de capacité.

Exemple d’utilisation de bandes de fractions :

Une boulangère vend \(\frac{3}{8}\) de ses pains le matin et \(\frac{1}{2}\) de ses pains le reste de la journée. À la fermeture, il lui reste 11 pains. Combien de pains avait-elle à l’ouverture du magasin?

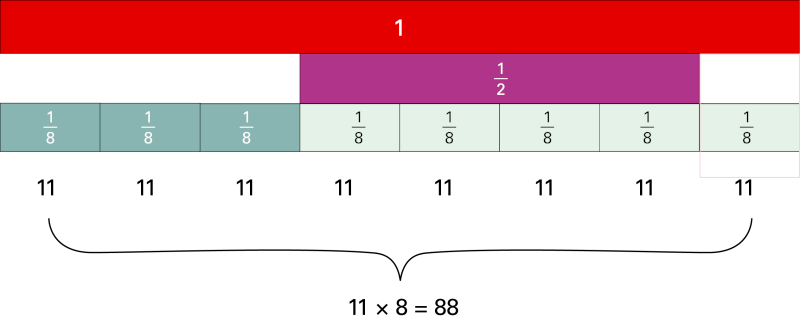
Huit chiffres onze sont placés horizontalement à intervalles réguliers. Au-dessus il y a 8 petites bandes de fractions, elles représentent les 8 fractions de : un sur 8, chacune des fractions est au-dessus des onze. Au-dessus des fractions il y a une bande de fractions de : une demie, elle prend l’espace de 4 bandes de : un sur 8. Puis une bande est placé au-dessus du : une demie elle représente un, la bande occupe l’espace au complet.

Il reste donc à la boulangère \(\frac{1}{8}\) de ses pains. Puisque \(\frac{1}{8}\) de ses pains restants correspond à 11 pains, elle avait \(11 \times 8 = 88\) pains à l’ouverture du magasin.